题目内容
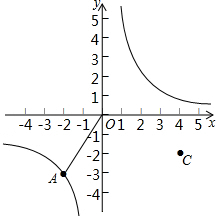 反比例函数
反比例函数 的图象经过点A(-2,-3),B是图象上在第一象限内的一个动点,
的图象经过点A(-2,-3),B是图象上在第一象限内的一个动点,
(1)求反比例函数解析式;
(2)直接写出当OA=OB时B点的坐标;
(3)已知点C(4,-2),当B点移动到何处时,四边形OACB为平行四边形?
解:(1)∵反比例函数 的图象经过点A(-2,-3),
的图象经过点A(-2,-3),
∴-3=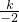 ,
,
解得:k=6,
∴反比例函数解析式的解析式为:y= ;
;
(2)∵点A(-2,-3),
∴OA2=13,
设点B的坐标为:(x, ),
),
∵OA=OB,
∴x2+( )2=13,
)2=13,
即x4-13x2+36=0,
∴(x2-4)(x2-9)=0,
解得:x=±2或x=±3,
∵B是图象上在第一象限内的一个动点,
∴x=2或x=3,
 ∴点B的坐标为:(2,3)或(3,2);
∴点B的坐标为:(2,3)或(3,2);
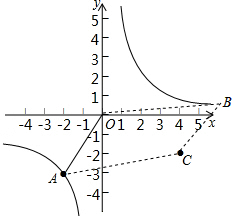
(3)∵四边形OACB为平行四边形,
∴OB∥AC,OA∥BC,OB=AC,OA=BC,
∴OB是由AC平移得到的;
∵点A(-2,-3),
∴OB向上平移了3个单位,向右平移了2个单位,
∵点C(4,-2),
∴点B的坐标为(6,1),
∴当B点移动到(6,1)时,四边形OACB为平行四边形.
分析:(1)由反比例函数 的图象经过点A(-2,-3),利用待定系数法,即可求得反比例函数解析式;
的图象经过点A(-2,-3),利用待定系数法,即可求得反比例函数解析式;
(2)由OA=OB,可设设点B的坐标为:(x, ),即可得方程:x2+(
),即可得方程:x2+( )2=13,解此方程即可求得答案;
)2=13,解此方程即可求得答案;
(3)由四边形OACB为平行四边形,可得OB是由AC平移得到的,继而求得答案.
点评:此题考查了待定系数法求反比例函数的解析式、反比例函数上点的特征以及平行四边形的性质.此题难度较大,注意掌握方程思想与数形结合思想的应用.
 的图象经过点A(-2,-3),
的图象经过点A(-2,-3),∴-3=
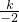 ,
,解得:k=6,
∴反比例函数解析式的解析式为:y=
 ;
;(2)∵点A(-2,-3),
∴OA2=13,
设点B的坐标为:(x,
 ),
),∵OA=OB,
∴x2+(
 )2=13,
)2=13,即x4-13x2+36=0,
∴(x2-4)(x2-9)=0,
解得:x=±2或x=±3,
∵B是图象上在第一象限内的一个动点,
∴x=2或x=3,
 ∴点B的坐标为:(2,3)或(3,2);
∴点B的坐标为:(2,3)或(3,2);(3)∵四边形OACB为平行四边形,
∴OB∥AC,OA∥BC,OB=AC,OA=BC,
∴OB是由AC平移得到的;
∵点A(-2,-3),
∴OB向上平移了3个单位,向右平移了2个单位,
∵点C(4,-2),
∴点B的坐标为(6,1),
∴当B点移动到(6,1)时,四边形OACB为平行四边形.
分析:(1)由反比例函数
 的图象经过点A(-2,-3),利用待定系数法,即可求得反比例函数解析式;
的图象经过点A(-2,-3),利用待定系数法,即可求得反比例函数解析式;(2)由OA=OB,可设设点B的坐标为:(x,
 ),即可得方程:x2+(
),即可得方程:x2+( )2=13,解此方程即可求得答案;
)2=13,解此方程即可求得答案;(3)由四边形OACB为平行四边形,可得OB是由AC平移得到的,继而求得答案.
点评:此题考查了待定系数法求反比例函数的解析式、反比例函数上点的特征以及平行四边形的性质.此题难度较大,注意掌握方程思想与数形结合思想的应用.

练习册系列答案
相关题目
已知反比例函数的图象经过点P(1,-2),则这个函数的图象位于( )
| A、第一、三象限 | B、第二、三象限 | C、第二、四象限 | D、第三、四象限 |