题目内容
【题目】如图,把一副三角板如图①放置,其中,∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=6cm,DC=7cm.把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图②).
(1)求∠OFE1的度数;
(2)求线段AD1的长.

【答案】(1)120°;(2)5.
【解析】
(1)利用已知得出∠BCO=45°,进而根据三角形内角和定理求出∠BOC的度数;
(2)根据OFE1=∠B+∠1,易得∠OFE1的度数,进而得出∠4=90°,在Rt△AD1O中根据勾股定理就可以求得AD1的长.
(1)如图乙所示,
∠BCO=60°-15°=45°,
∠BOC=180°-45°-45°=90°;
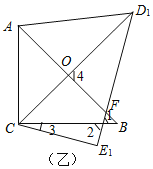
(2)如图乙所示,
∵∠3=15°,∠E1=90°,
∴∠1=∠2=75°,
又∵∠B=45°,
∴∠OFE1=∠B+∠1=45°+75°=120°;
∴∠D1FO=60°,
∵∠CD1E1=30°,
∴∠4=90°,
又∵AC=BC,∠A=45°
即△ABC是等腰直角三角形.
∴OA=OB=![]() AB=3cm,
AB=3cm,
∵∠ACB=90°,
∴CO=![]() AB=
AB=![]() ×6=3(cm),
×6=3(cm),
又∵CD1=7(cm),
∴OD1=CD1-OC=7-3=4(cm),
在Rt△AD1O中,AD1=![]() (cm)
(cm)

练习册系列答案
 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案
相关题目
【题目】在课堂上,老师将除颜色外都相同的1个黑球和若干个白球放入一个不透明的口袋并搅匀,让全班同学依次进行摸球试验,每次随机摸出一个球,记下颜色再放回搅匀,下表是试验得到的一组数据.
摸球的次数n | 100 | 150 | 200 | 500 | 800 |
摸到黑球的次数m | 26 | 37 | 49 | 124 | 200 |
摸到黑球的频率 |
|
|
|
| a |
![]() 表中a的值等于______;
表中a的值等于______;
![]() 估算口袋中白球的个数;
估算口袋中白球的个数;
![]() 用画树状图或列表的方法计算连续两名同学都摸出白球的概率.
用画树状图或列表的方法计算连续两名同学都摸出白球的概率.