题目内容
【题目】如图①，在平面直角坐标系中，
是函数
的图像上一点，
是y轴上一动点，四边形ABPQ是正方形（点A．B．P．Q按顺时针方向排列）。
（1）求a的值；
（2）如图②，当
时，求点P的坐标；
（3）若点P也在函数的图像上，求b的值；
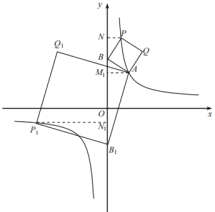
（4）设正方形ABPQ的中心为M，点N是函数的图像上一点，判断以点P．Q．M．N为顶点的四边形能否是正方形，如果能，请直接写出b的值，如果不能，请说明理由。
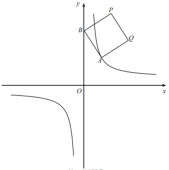
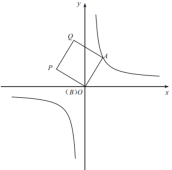
图① 图② 备用图
【答案】（1）
；（2）P的坐标为
.（3）
或
（4）
或
.
【解析】
（1）利用待定系数法即可解决问题．
（2）如图②中，作PE⊥x轴于E，AF⊥x轴于F．利用全等三角形的性质解决问题即可．
（3）如图③中，作AF⊥OB于F，PE⊥OB于E．利用全等三角形的性质求出点P的坐标，再利用待定系数法解决问题即可．
（4）如图④中，当点N在反比例函数图形上时，想办法用b表示点N的坐标，利用待定系数法解决问题即可．
（1）解：把
代入
，得
；
（2）解：如图①，过点A作
轴，垂足为M，过点P作
轴，垂足为T，
即
.
四边形ABPQ是正方形，
，
，
，
，
，
，
,
A的坐标为
，
，
，
P的坐标为.
（3）解：如图②
I．当
时，分别过点A、P作
轴、
轴，垂足为
、N.
与 （2）同理可证：
，
，
，
，
；
II．当
时，过点
作
轴，垂足为
.
同理：
，
，
综上所述，点P的坐标为
，
点P在反比例函数图像上，
，解得或
（4）或.
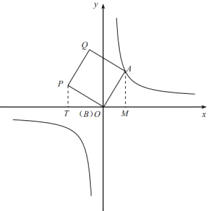
图① 图②
练习册系列答案
阅读快车系列答案
相关题目
