题目内容
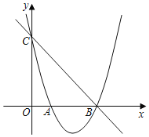
【题目】(2017·泰安)如图,是将抛物线![]() 平移后得到的抛物线,其对称轴为
平移后得到的抛物线,其对称轴为![]() ,与
,与![]() 轴的一个交点为
轴的一个交点为![]() ,另一交点为
,另一交点为![]() ,与
,与![]() 轴交点为
轴交点为![]() .
.

(1)求抛物线的函数表达式;
(2)若点![]() 为抛物线上一点,且
为抛物线上一点,且![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)点![]() 是抛物线上一点,点
是抛物线上一点,点![]() 是一次函数
是一次函数![]() 的图象上一点,若四边形
的图象上一点,若四边形![]() 为平行四边形,这样的点
为平行四边形,这样的点![]() 是否存在?若存在,分别求出点
是否存在?若存在,分别求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
【答案】(1)y=x2+2x+3;(2)(1,4);(3)P、Q的坐标是(0,3),(1,3)或(![]() ,
,![]() )、(
)、(![]() ,
,![]() ).
).
【解析】
(1)设抛物线的解析式是y=(x1)2+k.
把(1,0)代入得0=(11)2+k,解得k=4,
则抛物线的解析式是y=(x1)2+4,即y=x2+2x+3.
(2)在y=x2+2x+3中令x=0,得y=3,即C的坐标是(0,3),OC=3.
∵B的坐标是(3,0),∴OB=3,
∴OC=OB,则△OBC是等腰直角三角形.
∴∠OCB=45°,
过点N作NH⊥y轴,垂足是H.
∵∠NCB=90°,
∴∠NCH=45°,
∴NH=CH,
∴HO=OC+CH=3+CH=3+NH,
设点N的坐标是(a,a2+2a+3),
∴a+3=a2+2a+3,解得a=0(舍去)或a=1,
∴点N的坐标是(1,4).
(3)∵四边形OAPQ是平行四边形,则PQ=OA=1,且PQ∥OA,
设P(t,t2+2t+3),则t2+2t+3=![]() (t+1)+
(t+1)+![]() ,
,
整理,得2t2t=0,解得t=0或t=![]() .
.
∴t2+2t+3的值为3或![]() .
.
∴P、Q的坐标是(0,3),(1,3)或(![]() ,
,![]() )、(
)、(![]() ,
,![]() ).
).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某校初三进行了第三次模拟考试,该校领导为了了解学生的数学考试情况,抽样调查部分学生的数学成绩,并将抽样的数据进行了如下整理:
①如下分数段整理样本;
等级等级 | 分数段 | 各组总分 | 人数 |
A | 110<X<120 | P | 4 |
B | 100<X<110 | 843 | n |
C | 90<X≤100 | 574 | m |
D | 80<X<90 | 171 | 2 |
②根据左表绘制扇形统计图.

(1)填空m= ,n= ,数学成绩的中位数所在的等级 ;
(2)如果该校有1200名学生参加了本次模拟测,估计D等级的人数;
(3)已知抽样调查学生的数学成绩平均分为102分,求A等级学生的数学成绩的平均分数.
【题目】为了解某区初二年级数学学科期末质量监控情况,进行了抽样调查,过程如下,请将有关问题补充完整.收集数据:随机抽取甲乙两所学校的名学生的数学成绩进行
甲 91 89 77 86 71 31 97 93 72 91 81 92 85 85 95 88 88 90 44 91
乙 84 93 66 69 76 87 77 82 85 88 90 88 67 88 91 96 68 97 59 88
整理、描述数据:按如下数据段整理、描述这两组数据,分析数据:
分段 学校 |
|
|
|
|
|
|
|
甲 | 1 | 1 | 0 | 0 | 3 | 7 | 8 |
乙 |
两组数据的平均数、中位数、众数、方差如下表:
统计量 学校 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 81.85 |
| 91 | 268.43 |
乙 | 81.95 | 86 | 88 | 115.25 |
(1)经统计,表格中![]() 的值是__________.
的值是__________.
(2)得出结论
①若甲学校有600名初二学生,估计这次考试成绩80分以上人数为__________.
②可以推断出__________学校学生的数学水平较高,理由为:__________.(至少从两个不同的角度说明推断的合理性)