题目内容
已知：t1、t2是方程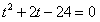
的两个实数根，且t1<t2，抛物线
的图象经过点
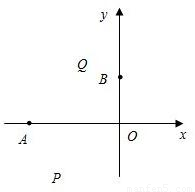
A（t1，0），B（0，t2）。
（1）求这个抛物线的解析式；
（2）设点P（x，y）是抛物线上一动点，且位于第三象限，四边形OPAQ是以OA为对角线的平行四边形，求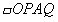
的面积S与x之间的函数关系式，并写出自变量的取值范围；
（3）在（2）的条件下，当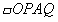
的面积为24时，是否存在这样的点P，使
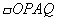为正方形？若存在，求出P点坐标；若不存在，说明理由。
（2）设点P（x，y）是抛物线上一动点，且位于第三象限，四边形OPAQ是以OA为对角线的平行四边形，求
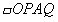的面积S与x之间的函数关系式，并写出自变量的取值范围；（3）在（2）的条件下，当
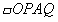的面积为24时，是否存在这样的点P，使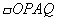为正方形？若存在，求出P点坐标；若不存在，说明理由。解：（1）抛物线的解析式为：
；
（2）∵点P（x，y）在抛物线上，位于第三象限，
∴y<0，即-y>0，
又∵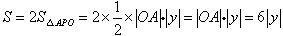
，
∴
，
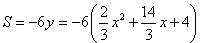
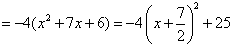令y=0，即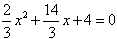
，解得：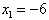
，
，
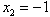∵抛物线与x轴的交点坐标为（-6，0），（-1，0），
∴x的取值范围为-6<x<-1。
（3）当S=24时，即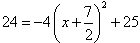
，解得：x1=-3，x2=-4，
代入解析式得：y1=-4，y2=-4，点P的坐标为（-3，-4），（-4，-4），
当点P为（-3，-4）时，满足PO=PA，此时，平行四边形OPAQ是菱形；
当点P为（-4，-4）时，不满足PO=PA，此时，此时，平行四边形OPAQ不是菱形，
而要使平行四边形OPAQ为正方形，那么，一定有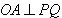
，
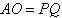，此时，点P的坐标为
（-3，-3），而（-3，-3）不在抛物线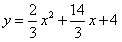
上，故不存在这样的点P，使四边形OPAQ为正方形。
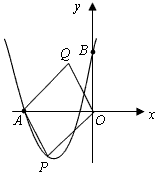
；（2）∵点P（x，y）在抛物线上，位于第三象限，
∴y<0，即-y>0，
又∵
，∴
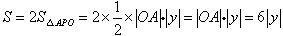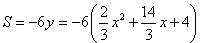
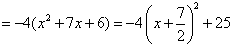，令y=0，即
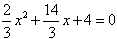，解得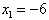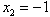：，，∵抛物线与x轴的交点坐标为（-6，0），（-1，0），
∴x的取值范围为-6<x<-1。
（3）当S=24时，即
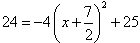，解得：x1=-3，x2=-4，代入解析式得：y1=-4，y2=-4，点P的坐标为（-3，-4），（-4，-4），
当点P为（-3，-4）时，满足PO=PA，此时，平行四边形OPAQ是菱形；
当点P为（-4，-4）时，不满足PO=PA，此时，此时，平行四边形OPAQ不是菱形，
而要使平行四边形OPAQ为正方形，那么，一定有
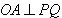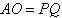，，此时，点P的坐标为（-3，-3），而（-3，-3）不在抛物线
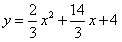上，故不存在这样的点P，使四边形OPAQ为正方形。
练习册系列答案
相关题目
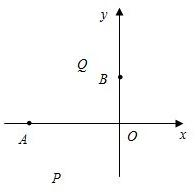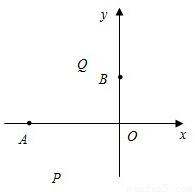
象经过点A（t1，0），B（0，t2）．
x2+bx+c的图象经过点A（t1，0），B（0，t2）．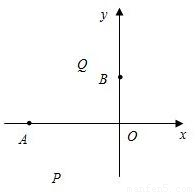
x2+bx+c的图象经过点A（t1，0），B（0，t2）．
x2+bx+c的图象经过点A（t1，0），B（0，t2）．