题目内容
已知:t1,t2是方程t2+2t-24=0的两个实数根,且t1<t2,抛物线y= x2+bx+c的图象经过点A(t1,0),B(0,t2).
x2+bx+c的图象经过点A(t1,0),B(0,t2).(1)求这个抛物线的解析式;
(2)设点P(x,y)是抛物线上一动点,且位于第三象限,四边形OPAQ是以OA为对角线的平行四边形,求平行四边形OPAQ的面积S与x之间的函数关系式,并写出自变量x的取值范围;
(3)在(2)的条件下,当平行四边形OPAQ的面积为24时,是否存在这样的点P,使?OPAQ为正方形?若存在,求出P点坐标;若不存在,说明理由.
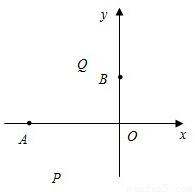
【答案】分析:(1)解方程t2+2t+24=0,可得A(-6,0),B(0,4),再利用待定系数法求二次函数的解析式;
(2)设点P(x,y),利用x,y表示四边形的边长求得面积S=-4(x+ )2+25,利用面积是正数的性质求出x的取值范围是-6<x<-1;
)2+25,利用面积是正数的性质求出x的取值范围是-6<x<-1;
(3)把S=24代入解析式S=-4(x+ )2+25中求得y的值,从而得到点P的坐标,根据实际意义进行值的取舍,讨论可知不存在这样的点P,使四边形OPAQ为正方形.
)2+25中求得y的值,从而得到点P的坐标,根据实际意义进行值的取舍,讨论可知不存在这样的点P,使四边形OPAQ为正方形.
解答: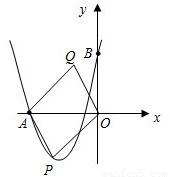 解:
解:
(1)t2+2t-24=0,(t+6)(t-4)=0,t1=-6,t2=4(1分)
∵t1<t2,
∴A(-6,0),B(0,4)(2分)
∵抛物线y= x2+bx+c经过A,B两点.
x2+bx+c经过A,B两点.
∴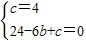 ,
,
解得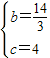 ,
,
∴y= x2+
x2+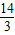 x+4.(4分)
x+4.(4分)
(2)∵点P(x,y)在抛物线上,位于第三象限,
∴y<0,即-y>0.
又∵S=2S△APO=2× ×|OA|•|y|=|OA|•|y|=6|y|,
×|OA|•|y|=|OA|•|y|=6|y|,
∴S=-6y(6分)
=-6( x2+
x2+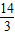 x+4)
x+4)
=-4(x2+7x+6)
=-4(x+ )2+25(7分)
)2+25(7分)
令y=0时, x2+
x2+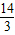 x+4=0,
x+4=0,
解得x1=-6,x2=-1.
∵抛物线与x轴的交点坐标为(-6,0),(-1,0),
∴x的取值范围为-6<x<-1.(8分)
(3)当S=24时,得24=-4(x+ )2+25,
)2+25,
解得:x1=-3,x2=-4(9分)
代入解析式得:y1=-4,y2=-4.
∴点P的坐标为(-3,-4),(-4,-4)
当点P为(-3,-4)时,满足PO=PA,此时,平行四边形OPAQ是菱形.
当点P为(-4,-4)时,不满足PO=PA,此时,平行四边形OPAQ不是菱形.(10分)
而要使平行四边形OPAQ为正方形,那么,一定有OA⊥PQ,AO=PQ,
此时,点P的坐标为(-3,-3),而(-3,-3)不在抛物线y= x2+
x2+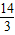 x+4上,
x+4上,
故不存在这样的点P,使四边形OPAQ为正方形.(12分)
点评:主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养.
要会利用数形结合的思想把代数和几何图形结合起来,利用点的坐标的意义表示线段的长度,从而求出线段之间的关系.
(2)设点P(x,y),利用x,y表示四边形的边长求得面积S=-4(x+
 )2+25,利用面积是正数的性质求出x的取值范围是-6<x<-1;
)2+25,利用面积是正数的性质求出x的取值范围是-6<x<-1;(3)把S=24代入解析式S=-4(x+
 )2+25中求得y的值,从而得到点P的坐标,根据实际意义进行值的取舍,讨论可知不存在这样的点P,使四边形OPAQ为正方形.
)2+25中求得y的值,从而得到点P的坐标,根据实际意义进行值的取舍,讨论可知不存在这样的点P,使四边形OPAQ为正方形.解答:
 解:
解:(1)t2+2t-24=0,(t+6)(t-4)=0,t1=-6,t2=4(1分)
∵t1<t2,
∴A(-6,0),B(0,4)(2分)
∵抛物线y=
 x2+bx+c经过A,B两点.
x2+bx+c经过A,B两点.∴
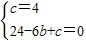 ,
,解得
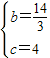 ,
,∴y=
 x2+
x2+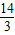 x+4.(4分)
x+4.(4分)(2)∵点P(x,y)在抛物线上,位于第三象限,
∴y<0,即-y>0.
又∵S=2S△APO=2×
 ×|OA|•|y|=|OA|•|y|=6|y|,
×|OA|•|y|=|OA|•|y|=6|y|,∴S=-6y(6分)
=-6(
 x2+
x2+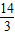 x+4)
x+4)=-4(x2+7x+6)
=-4(x+
 )2+25(7分)
)2+25(7分)令y=0时,
 x2+
x2+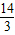 x+4=0,
x+4=0,解得x1=-6,x2=-1.
∵抛物线与x轴的交点坐标为(-6,0),(-1,0),
∴x的取值范围为-6<x<-1.(8分)
(3)当S=24时,得24=-4(x+
 )2+25,
)2+25,解得:x1=-3,x2=-4(9分)
代入解析式得:y1=-4,y2=-4.
∴点P的坐标为(-3,-4),(-4,-4)
当点P为(-3,-4)时,满足PO=PA,此时,平行四边形OPAQ是菱形.
当点P为(-4,-4)时,不满足PO=PA,此时,平行四边形OPAQ不是菱形.(10分)
而要使平行四边形OPAQ为正方形,那么,一定有OA⊥PQ,AO=PQ,
此时,点P的坐标为(-3,-3),而(-3,-3)不在抛物线y=
 x2+
x2+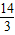 x+4上,
x+4上,故不存在这样的点P,使四边形OPAQ为正方形.(12分)
点评:主要考查了二次函数的解析式的求法和与几何图形结合的综合能力的培养.
要会利用数形结合的思想把代数和几何图形结合起来,利用点的坐标的意义表示线段的长度,从而求出线段之间的关系.

练习册系列答案
相关题目
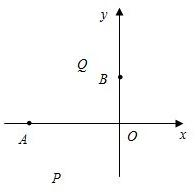 象经过点A(t1,0),B(0,t2).
象经过点A(t1,0),B(0,t2). x2+bx+c的图象经过点A(t1,0),B(0,t2).
x2+bx+c的图象经过点A(t1,0),B(0,t2).
 x2+bx+c的图象经过点A(t1,0),B(0,t2).
x2+bx+c的图象经过点A(t1,0),B(0,t2).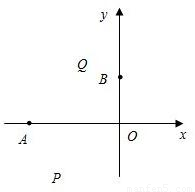
 x2+bx+c的图象经过点A(t1,0),B(0,t2).
x2+bx+c的图象经过点A(t1,0),B(0,t2).
 x2+bx+c的图象经过点A(t1,0),B(0,t2).
x2+bx+c的图象经过点A(t1,0),B(0,t2).