题目内容
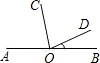 如图所示,点O是直线AB上的点,OC平分∠AOD,∠BOD=30°,则∠AOC=
如图所示,点O是直线AB上的点,OC平分∠AOD,∠BOD=30°,则∠AOC=分析:根据图示,求出∠AOD的度数,然后利用角平分线的性质,求出∠AOC的度数.
解答:解:∵∠BOD=30°,
∴∠AOD=180°-∠BOD=180°-30°=150°,
∵OC平分∠AOD,
∴∠AOC=
∠AOD=75°.
故答案为75°.
∴∠AOD=180°-∠BOD=180°-30°=150°,
∵OC平分∠AOD,
∴∠AOC=
| 1 |
| 2 |
故答案为75°.
点评:此题考查角的运算,运用了平角和角平分线的定义.

练习册系列答案
相关题目
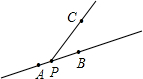 如图所示,点P是直线AB上的一个运动点,点C是直线AB外一固定的点,则下列描述正确的是( )
如图所示,点P是直线AB上的一个运动点,点C是直线AB外一固定的点,则下列描述正确的是( )| A、在点P的运动过程中,使直线PC⊥AB的点P有两个 | B、若∠CBA>90°,当点P从A出发,沿射线AB的方向运动时,∠CPB不断变大 | C、若AB=2AP,则点P是线段AB的中点 | D、当∠CPA=90°时,线段CP的长度就是点C到直线AB的距离 |
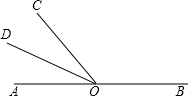 解:∵O是直线AB上一点
解:∵O是直线AB上一点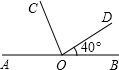 如图所示,点O是直线AB上的点,OC平分∠AOD,∠BOD=40°,则∠AOC=
如图所示,点O是直线AB上的点,OC平分∠AOD,∠BOD=40°,则∠AOC=