题目内容
已知:关于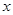 的一元二次方程
的一元二次方程 (m为实数)
(m为实数)
【小题1】若方程有两个不相等的实数根,求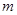 的取值范围;
的取值范围;
【小题2】在(1)的条件下,求证:无论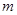 取何值,抛物线
取何值,抛物线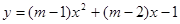 总过
总过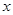 轴上的一个固定点;
轴上的一个固定点;
【小题3】若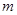 是整数,且关于
是整数,且关于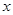 的一元二次方程
的一元二次方程 有两个不相等的整数根,把抛物线
有两个不相等的整数根,把抛物线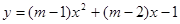 向右平移3个单位长度,求平移后的解析式.
向右平移3个单位长度,求平移后的解析式.
【小题1】(1)△=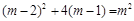 ∵方程有两个不相等的实数根,
∵方程有两个不相等的实数根,
∴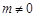 .∵
.∵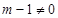 ,∴m的取值范围是
,∴m的取值范围是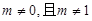
【小题2】证明:令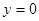 得,
得,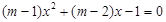 .
.
∴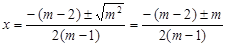 .[ ∴
.[ ∴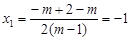 ,
,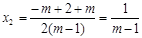 .∴抛物线与x轴的交点坐标为(
.∴抛物线与x轴的交点坐标为(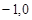 ),(
),(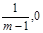 ),
),
∴无论m取何值,抛物线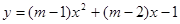 总过定点(
总过定点(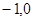 )
)
【小题3】∵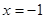 是整数 ∴只需
是整数 ∴只需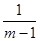 是整数.∵
是整数.∵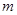 是整数,且
是整数,且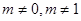 ,
,
∴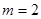 .当
.当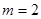 时,抛物线为
时,抛物线为 .
.
把它的图象向右平移3个单位长度,得到的抛物线解析式为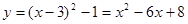 .
.
解析

练习册系列答案
相关题目

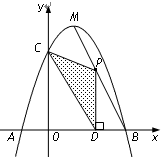
 (12分)如图,已知关于
(12分)如图,已知关于 的一元二次函数
的一元二次函数 (
( )的图象与
)的图象与 、
、 两点(点
两点(点 轴交于点
轴交于点 ,且
,且 ,顶点为
,顶点为 .
.
 点
点 为线段
为线段 上的一个动点,过点
上的一个动点,过点 ,垂足为
,垂足为 .若
.若 ,
, 的面积为
的面积为 ,求
,求 的函数关系式,并写出
的函数关系式,并写出 的一元二次函数
的一元二次函数 (
( )的图象与
)的图象与 、
、 两点(点
两点(点 轴交于点
轴交于点 ,且
,且 ,顶点为
,顶点为 .
.
 为线段
为线段 上的一个动点,过点
上的一个动点,过点 ,垂足为
,垂足为 .若
.若 ,
, 的面积为
的面积为 ,求
,求 的函数关系式,并写出
的函数关系式,并写出 点坐标是 时,
点坐标是 时,  的一元二次函数
的一元二次函数 (
( )的图象与
)的图象与 、
、 两点(点
两点(点 轴交于点
轴交于点 ,且
,且 ,顶点为
,顶点为 .
.
 为线段
为线段 上的一个动点,过点
上的一个动点,过点 ,垂足为
,垂足为 .若
.若 ,
, 的面积为
的面积为 ,求
,求 的函数关系式,并写出
的函数关系式,并写出 点坐标是 时,
点坐标是 时, 的一元二次函数
的一元二次函数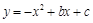 (
( )的图象与
)的图象与 、
、 两点(点
两点(点 轴交于点
轴交于点 ,且
,且 ,顶点为
,顶点为 .
.
 为线段
为线段 上的一个动点,过点
上的一个动点,过点 ,垂足为
,垂足为 .若
.若 ,
, 的面积为
的面积为 ,求
,求 的函数关系式,并写出
的函数关系式,并写出 点坐标是 时,
点坐标是 时,