题目内容
【题目】在△ABC中，AB=AC，BD=CD，∠BAD=40°，AD=AE．求∠CDE的度数．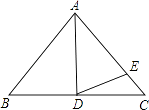 
【答案】解：∵AB=AC，
∴△ABC为等腰三角形，
∵AD=AE，
∴△ADE为等腰三角形，
∵∠BAD=40°，
∴∠DAE=40°，
∴∠ADE= 
（180°﹣∠DAE）= （180°﹣40°）=70°，
又∵△ABC为等腰三角形，BD=CD，
∴AD⊥CD（三线合一），
∴∠CDE=90°﹣∠ADE=90°﹣70°=20°．
故答案为：20°
【解析】首先得到△ABC，△ADE均为等腰三角形，再根据等腰三角形的性质求解．
【考点精析】通过灵活运用三角形的内角和外角，掌握三角形的三个内角中，只可能有一个内角是直角或钝角；直角三角形的两个锐角互余；三角形的一个外角等于和它不相邻的两个内角的和；三角形的一个外角大于任何一个和它不相邻的内角即可以解答此题．
练习册系列答案
阅读快车系列答案
相关题目
【题目】某公司为了解员工对“六五”普法知识的知晓情况，从本公司随机选取40名员工进行普法知识考查，对考查成绩进行统计（成绩均为整数，满分100分），并依据统计数据绘制了如下尚不完整的统计表．解答下列问题：
（1） 表中a＝__________，b＝__________，c＝__________
（2） 请补全频数分布直方图
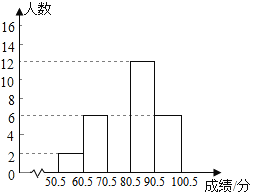
（3）该公司共有员工3000人，若考查成绩80分以上（不含80分）为优秀，试估计该公司员工“六五”普法知识知晓程度达到优秀的人数
组别 | 分数段/分 | 频数/人数 | 频率 |
1 | 50.5~60.5 | 2 | a |
2 | 60.5~70.5 | 6 | 0.15 |
3 | 70.5~80.5 | b | c |
4 | 80.5~90.5 | 12 | 0.30 |
5 | 90.5~100.5 | 6 | 0.15 |
合计 | 40 | 1.00 | |
