Question

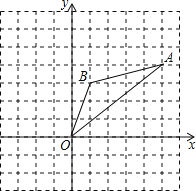
【题目】在如图的直角坐标系中，已知点A(2,0)、B(0，－4)，将线段AB绕点A按逆时针方向旋转90°至AC．

(1)求点C的坐标；

(2)若抛物线y＝－x2＋ax＋4经过点C．

①求抛物线的解析式；

②在抛物线上是否存在点P(点C除外)使△ABP是以AB为直角边的等腰直角三角形?若存在，求出所有点P的坐标；若不存在，请说明理由．

Answer 1

【答案】C的坐标为（3，﹣1）；

（2）①抛物线的解析式为y=﹣x2+x+2；

②存在点P，△ABP是以AB为直角边的等腰直角三角形，符合条件的点有P1（﹣1，1），P2（﹣2，﹣1）两点．

【解析】

试题（1）过点C作CD垂直于x轴，由线段AB绕点A按逆时针方向旋转90°至AC，根据旋转的旋转得到AB=AC，且∠BAC为直角，可得∠OAB与∠CAD互余，由∠AOB为直角，可得∠OAB与∠ABO互余，根据同角的余角相等可得一对角相等，再加上一对直角相等，利用ASA可证明三角形ACD与三角形AOB全等，根据全等三角形的对应边相等可得AD=OB，CD=OA，由A和B的坐标及位置特点求出OA及OB的长，可得出OD及CD的长，根据C在第四象限得出C的坐标；

（2）①由已知的抛物线经过点C，把第一问求出C的坐标代入抛物线解析式，列出关于a的方程，求出方程的解得到a的值，确定出抛物线的解析式；

②假设存在点P使△ABP是以AB为直角边的等腰直角三角形，分三种情况考虑：（i）A为直角顶点，过A作AP1垂直于AB，且AP1=AB，过P1作P1M垂直于x轴，如图所示，根据一对对顶角相等，一对直角相等，AB=AP1，利用AAS可证明三角形AP1M与三角形ACD全等，得出AP1与P1M的长，再由P1为第二象限的点，得出此时P1的坐标，代入抛物线解析式中检验满足；（ii）当B为直角顶点，过B作BP2垂直于BA，且BP2=BA，过P2作P2N垂直于y轴，如图所示，同理证明三角形BP2N与三角形AOB全等，得出P2N与BN的长，由P2为第三象限的点，写出P2的坐标，代入抛物线解析式中检验满足；（iii）当B为直角顶点，过B作BP3垂直于BA，且BP3=BA，如图所示，过P3作P3H垂直于y轴，同理可证明三角形P3BH全等于三角形AOB，可得出P3H与BH的长，由P3为第四象限的点，写出P3的坐标，代入抛物线解析式检验，不满足，综上，得到所有满足题意的P的坐标．

试题解析：（1）过C作CD⊥x轴，垂足为D，

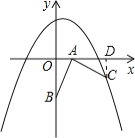
∵BA⊥AC，∴∠OAB+∠CAD=90°，

又∠AOB=90°，∴∠OAB+∠OBA=90°，

∴∠CAD=∠OBA，又AB=AC，∠AOB=∠ADC=90°，

∴△AOB≌△CDA，又A（1，0），B（0，﹣2），

∴OA=CD=1，OB=AD=2，

∴OD=OA+AD=3，又C为第四象限的点，

∴C的坐标为（3，﹣1）；

（2）①∵抛物线y=﹣x2+ax+2经过点C，且C（3，﹣1），

∴把C的坐标代入得：﹣1=﹣+3a+2，解得：a=，

则抛物线的解析式为y=﹣x2+x+2；

②存在点P，△ABP是以AB为直角边的等腰直角三角形，

（i）若以AB为直角边，点A为直角顶点，

则延长CA至点P1使得P1A=CA，得到等腰直角三角形ABP1，过点P1作P1M⊥x轴，如图所示，

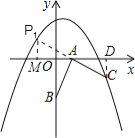
∵AP1=CA，∠MAP1=∠CAD，∠P1MA=∠CDA=90°，

∴△AMP1≌△ADC，

∴AM=AD=2，P1M=CD=1，

∴P1（﹣1，1），经检验点P1在抛物线y=﹣x2+x+2上；

（ii）若以AB为直角边，点B为直角顶点，则过点B作BP2⊥BA，且使得BP2=AB，

得到等腰直角三角形ABP2，过点P2作P2N⊥y轴，如图，

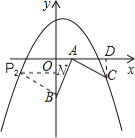
同理可证△BP2N≌△ABO，

∴NP2=OB=2，BN=OA=1，

∴P2（﹣2，﹣1），经检验P2（﹣2，﹣1）也在抛物线y=﹣x2+x+2上；

（iii）若以AB为直角边，点B为直角顶点，则过点B作BP3⊥BA，且使得BP3=AB，

得到等腰直角三角形ABP3，过点P3作P3H⊥y轴，如图，

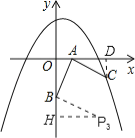
同理可证△BP3H≌△BAO，

∴HP3=OB=2，BH=OA=1，

∴P3（2，﹣3），经检验P3（2，﹣3）不在抛物线y=﹣x2+x+2上；

则符合条件的点有P1（﹣1，1），P2（﹣2，﹣1）两点．