Question

【题目】（1）已知实数a、b在数轴上的位置如图所示,化简=_____________；

（2）已知正整数，满足，则整数对的个数是_______________；

（3）△ABC中,∠A=50°,高BE、CF所在的直线交于点O,∠BOC的度数__________.

Answer 1

【答案】（1）2a－2b＋1；（2）3；（3）130°或50°.

【解析】（1）∵-1<a<0,b>1,

∴

＝|a+1|-|a-2b|

=1+a-2b+a

=2a-2b+1.

(2)∵，

∴，p=2016-6+9q,

∴p=14x3(其中x为正整数)，

同理可得：q=14y2（其中y为正整数）,

则x+3y=12(x、y为正整数)

∴,

∴整数对有（p,q）=(1481,14),或（14 ,或（）。

∴满足条件的整数对有3对.

(3)①当交点在三角形内部时（如图1），

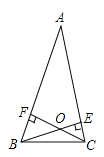
在四边形AFOE中，∠AFC=∠AEB=90°，∠A=50°，
根据四边形内角和等于360°得，
∠EOF=180°-∠A=180°-50°=130°，
故∠BOC=130°；

②当交点在三角形外部时（如图2），

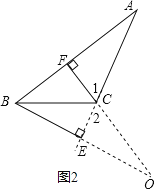
在△AFC中，∠A=50°，∠AFC=90°，
故∠1=180°-90°-50°=40°，
∵∠1=∠2，
∴在△CEO中，∠2=40°，∠CEO=90°，
∴∠EOF=180°-90°-40°=70°，
即∠BOC=50°，
综上所述：∠BOC的度数是130°或50°．
故答案是：(1). 2a－2b＋1 (2). 3 (3). 130°或50°．