题目内容
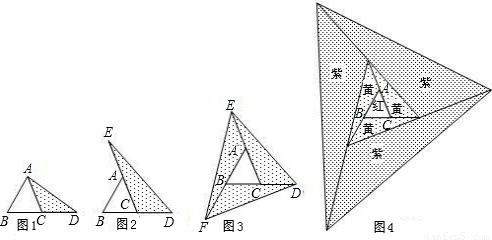
(2006•河北)探索:在如图1至图3中,△ABC的面积为a.
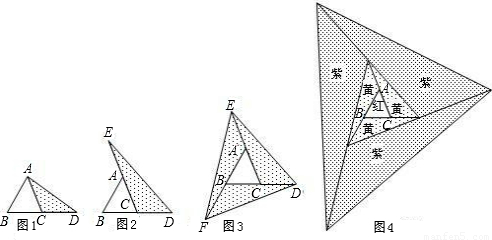
(1)如图1,延长△ABC的边BC到点D,使CD=BC,连接DA.若△ACD的面积为S1,则S1=______(用含a的代数式表示);
(2)如图2,延长△ABC的边BC到点D,延长边CA到点E,使CD=BC,AE=CA,连接DE.若△DEC的面积为S2,则S2=______(用含a的代数式表示),并写出理由;
(3)在图2的基础上延长AB到点F,使BF=AB,连接FD,FE,得到△DEF(如图3).若阴影部分的面积为S3,则S3=______(用含a的代数式表示).
发现:
像上面那样,将△ABC各边均顺次延长一倍,连接所得端点,得到△DEF(如图3),此时,我们称△ABC向外扩展了一次.可以发现,扩展一次后得到的△DEF的面积是原来△ABC面积的______倍.
应用:
去年在面积为10m2的△ABC空地上栽种了某种花卉.今年准备扩大种植规模,把△ABC向外进行两次扩展,第一次由△ABC扩展成△DEF,第二次由△DEF扩展成△MGH(如图4).求这两次扩展的区域(即阴影部分)面积共为多少m2?
【答案】分析:(1)根据三角形的面积公式,得到等底同高的两个三角形的面积相等;
(2)运用分割法:连接AD.根据三角形的面积公式进行分析:等底同高的两个三角形的面积相等;
(3)在(2)的基础上,阴影部分的面积是(2)中求得的面积的3倍;再加上原来三角形的面积进行计算.
应用:根据上述结论,即扩展一次后得到的三角形的面积是原三角形的面积的7倍,则扩展两次后,得到的三角形的面积是原三角形的面积的72=49倍.从而得到扩展的区域的面积是原来的48倍.
解答:解:(1)∵BC=CD,
∴△ACD和△ABC是等底同高的,即S1=a;
(2)2a;(2分)
理由:连接AD,
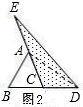
∵CD=BC,AE=CA,
∴S△DAC=S△DAE=S△ABC=a,
∴S2=2a;
(3)结合(2)得:2a×3=6a;
扩展一次后得到的△DEF的面积是6a+a=7a,即是原来三角形的面积的7倍.
应用拓展区域的面积:(72-1)×10=480(m2).
点评:命题立意:考查学生探索知识、发现知识、应用知识的综合创新能力.
点评:本题的探索过程由简到难,运用类比方法可依次求出.从而使考生在身临数学的情境中潜移默化,逐渐感悟到数学思维的力量,使学生对知识的发生及发展过程,解题思想方法的感悟,体会得淋漓尽致,是一道新课标理念不可多得的好题.
(2)运用分割法:连接AD.根据三角形的面积公式进行分析:等底同高的两个三角形的面积相等;
(3)在(2)的基础上,阴影部分的面积是(2)中求得的面积的3倍;再加上原来三角形的面积进行计算.
应用:根据上述结论,即扩展一次后得到的三角形的面积是原三角形的面积的7倍,则扩展两次后,得到的三角形的面积是原三角形的面积的72=49倍.从而得到扩展的区域的面积是原来的48倍.
解答:解:(1)∵BC=CD,
∴△ACD和△ABC是等底同高的,即S1=a;
(2)2a;(2分)
理由:连接AD,

∵CD=BC,AE=CA,
∴S△DAC=S△DAE=S△ABC=a,
∴S2=2a;
(3)结合(2)得:2a×3=6a;
扩展一次后得到的△DEF的面积是6a+a=7a,即是原来三角形的面积的7倍.
应用拓展区域的面积:(72-1)×10=480(m2).
点评:命题立意:考查学生探索知识、发现知识、应用知识的综合创新能力.
点评:本题的探索过程由简到难,运用类比方法可依次求出.从而使考生在身临数学的情境中潜移默化,逐渐感悟到数学思维的力量,使学生对知识的发生及发展过程,解题思想方法的感悟,体会得淋漓尽致,是一道新课标理念不可多得的好题.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目

 ,则
,则
 =________(用含a的代数式表示),并写出理由;
=________(用含a的代数式表示),并写出理由;
 ,则
,则
 的△ABC空地上栽种了某种花卉,今年准备扩大种植规模,把△ABC向外进行两次扩展,第一次由△ABC扩展成△DEF,第二次由△DEF扩展成△MGH(如图4),求这两次扩展的区域(即阴影部分)面积共为多少
的△ABC空地上栽种了某种花卉,今年准备扩大种植规模,把△ABC向外进行两次扩展,第一次由△ABC扩展成△DEF,第二次由△DEF扩展成△MGH(如图4),求这两次扩展的区域(即阴影部分)面积共为多少