题目内容
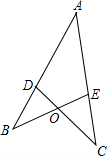如图，在△ABE与△ACD中，点D在AB上，点E在AC上，BE和CD相交于点O，若AB=AC，BD=CE则∠ADC=∠AEB．请说明理由．分析：求出AD=AE，根据SAS证△ADC≌△AEB，根据全等三角形的性质推出即可．
解答：解：∠ADC=∠AEB，
理由是：∵AB=AC，BD=CE，
∴AB-BD=AC-CE，
∴AD=AE，
在△ADC和△AEB中
∴△ADC≌△AEB（SAS），
∴∠ADC=∠AEB．
理由是：∵AB=AC，BD=CE，
∴AB-BD=AC-CE，
∴AD=AE，
在△ADC和△AEB中
|
∴△ADC≌△AEB（SAS），
∴∠ADC=∠AEB．
点评：本题考查了全等三角形的性质和判定的综合应用．
练习册系列答案
相关题目
25、如图，在△ABE中，AB=AE，将△ABE沿直线BE平移到△DEC的位置，连接AD．
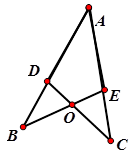
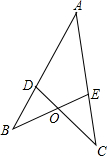如图，在△ABE与△ACD中，点D在AB上，点E在AC上，BE和CD相交于点O，若AB=AC，BD=CE则∠ADC=∠AEB．请说明理由．