题目内容
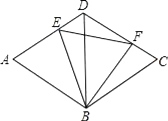
【题目】如图,菱形ABCD的边长为2,BD=2,E、F分别是边AD,CD上的两个动点,且满足AE+CF=2.
(1)求证:△BDE≌△BCF;
(2)判断△BEF的形状,并说明理由.
【答案】(1)证明见解析(2)等边三角形
【解析】试题分析:(1)由菱形ABCD的边长为2,BD=2,易得BD=BC,∠C=∠BDE=60°,又由AE+CF=2,易得DE=CF,则可证得:△BDE≌△BCF;
(2)由△BDE≌△BCF,易得BE=BF,∠EBF=60°,则可证得△BEF是等边三角形.
试题解析:(1)证明:∵菱形ABCD的边长为2,BD=2,∴BC=BD=CD=AD=2,∴∠C=∠CDB=60°.∵∠BDE=∠BDC,∴∠BDE=∠C.∵AE+DE=AD=2,AE+CF=2,∴DE=CF.在△BDE和△BCF中,∵BD=BC,∠BDE=∠C,DE=CF,∴△BDE≌△BCF(SAS);
(2)解:等边三角形.理由如下:
∵△BDE≌△BCF,∴BE=BF,∠CBF=∠DBE.∵∠CBF+∠DBF=60°,∴∠EBF=∠EBD+∠DBF=∠CBF+∠DBF=60°,∴△BEF是等边三角形.

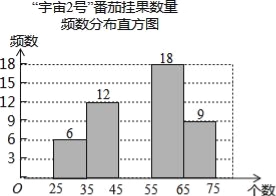
【题目】在太空种子种植体验实践活动中,为了解“宇番2号”番茄,某校科技小组随机调查60株番茄的挂果数量x(单位:个),并绘制如下不完整的统计图表:
“宇番2号”番茄挂果数量统计表
挂果数量x(个) | 频数(株) | 频率 |
25≤x<35 | 6 | 0.1 |
35≤x<45 | 12 | 0.2 |
45≤x<55 | a | 0.25 |
55≤x<65 | 18 | b |
65≤x<75 | 9 | 0.15 |
请结合图表中的信息解答下列问题:
(1)统计表中,a= ,b= ;
(2)将频数分布直方图补充完整;
(3)若绘制“番茄挂果数量扇形统计图”,则挂果数量在“35≤x<45”所对应扇形的圆心角度数为 °;
(4)若所种植的“宇番2号”番茄有1000株,则可以估计挂果数量在“55≤x<65”范围的番茄有 株.