Question

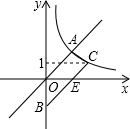如图，梯形AOBC的顶点A，C在反比例函数图象上，OA∥BC，上底边OA在直线y=x上，下底边BC交x轴于E（2，0），则四边形AOEC的面积为（　　）

• A、3
• B、

  3

• C、

  3

  -1
• D、

  3

  +1

Answer 1

分析：四边形AOEC的面积=梯形AOBC的面积-三角形OBE的面积．
根据AO∥BC，且直线BC经过E（2，0），用待定系数法求出BE的解析式，再求出B、C两点的坐标．根据C点坐标得出反比例函数解析式为y=

3

x

，解方程组

y=x y= 3 x

，求出A点坐标．根据勾股定理求出OA、BC的长度，易求梯形AOBC的高，从而求出梯形AOBC的面积．△OBE是等腰直角三角形，腰长是2，易求其面积．

解答：解：因为AO∥BC，上底边OA在直线y=x上，
则可设BE的解析式为y=x+b，
将E（2，0）代入上式得，b=-2，
BE的解析式为y=x-2．
把y=1代入y=x-2，得x=3，C点坐标为（3，1），
则反比例函数解析式为y=

3

x

，
将它与y=x组成方程组得：

y=x y= 3 x

，
解得x=

3

，x=-

3

（负值舍去）．
代入y=x得，y=

3

．
A点坐标为（

3

，

3

），
OA=

( 3 )2+( 3 )2

=

6

，
BC=

32+32

=3

2

，
∵B（0，-2），E（2，0），
∴BE=2

2

，
∴BE边上的高为

2

，
∴梯形AOBC高为：

2

，
梯形AOBC面积为：

1

2

×（3

2

+

6

）×

2

=3+

3

，
△OBE的面积为：

1

2

×2×2=2，
则四边形AOEC的面积为3+

3

-2=1+

3

．
故选D．

点评：此题综合考查了梯形和函数的有关知识，此题难度较大，考查了函数和方程的关系，交点坐标和方程组的解的关系，以及反比例函数系数k的几何意义．要用梯形、三角形的面积公式及勾股定理来计算．