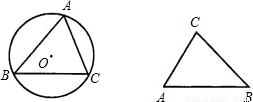题目内容
(2002•深圳)阅读材料,解答问题:命题:如图,在锐角△ABC中,BC=a,CA=b,AB=c,△ABC的外接圆半径为R,则
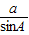 =
=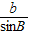 =
= =2R.
=2R.证明:连接CO并延长交⊙O于点D,连接DB,则∠D=∠A.
因为CD是⊙O的直径,所以∠DBC=90°,
在Rt△DBC中,sin∠D=
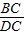 =
=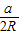 ,
,所以sinA=
 ,即
,即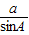 =2R,
=2R,同理:
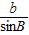 =2R,
=2R,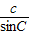 =2R,
=2R,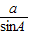 =
=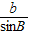 =
=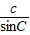 =2R,
=2R,请阅读前面所给的命题和证明后,完成下面(1)(2)两题:
(1)前面阅读材料中省略了“
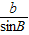 =2R,
=2R,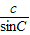 =2R”的证明过程,请你把“
=2R”的证明过程,请你把“ =2R”的证明过程补写出来.
=2R”的证明过程补写出来.(2)直接运用阅读材料中命题的结论解题,已知锐角△ABC中,BC=
 ,CA=
,CA= ,∠A=60°,求△ABC的外接圆半径R及∠C.
,∠A=60°,求△ABC的外接圆半径R及∠C.

【答案】分析:(1)根据已知的证明过程,同样可以分别把∠B和b;∠C和c构造到直角三角形中,根据锐角三角函数进行证明;
(2)根据(1)中证明的结论 =
= =
= =2R,代入计算.
=2R,代入计算.
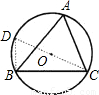
解答: (1)证明:连接CO并延长交⊙O于点D,连接DB,则∠A=∠D;
(1)证明:连接CO并延长交⊙O于点D,连接DB,则∠A=∠D;
因为CD是⊙O的直径,
所以∠DBC=90°,
在Rt△DBC中,
sin∠D= ,
,
所以sinB= ,即
,即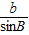 =2R;
=2R;
(2)解:由命题结论知
 =
= ,
,
∴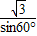 =
= ,
,
∴sinB=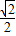 ;
;
∵BC>CA,
∴∠A>∠B,
∴∠B=45°,
∴∠C=75°.
由 =2R,得R=1.
=2R,得R=1.
点评:构造直径所对的圆周角,是圆中构造直角三角形常用的一种方法.熟记这一结论: =
= =
= =2R,便于计算.
=2R,便于计算.
(2)根据(1)中证明的结论
 =
= =
= =2R,代入计算.
=2R,代入计算.解答:
 (1)证明:连接CO并延长交⊙O于点D,连接DB,则∠A=∠D;
(1)证明:连接CO并延长交⊙O于点D,连接DB,则∠A=∠D;因为CD是⊙O的直径,
所以∠DBC=90°,
在Rt△DBC中,
sin∠D=
 ,
,所以sinB=
 ,即
,即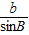 =2R;
=2R;(2)解:由命题结论知
 =
= ,
,∴
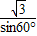 =
= ,
,∴sinB=
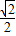 ;
;∵BC>CA,
∴∠A>∠B,
∴∠B=45°,
∴∠C=75°.
由
 =2R,得R=1.
=2R,得R=1.点评:构造直径所对的圆周角,是圆中构造直角三角形常用的一种方法.熟记这一结论:
 =
= =
= =2R,便于计算.
=2R,便于计算. 
练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
 在平面直角坐标系中,已知两点坐标P1(x1,y1)P2(x2,y2)我们就可以使用两点间距离公式
在平面直角坐标系中,已知两点坐标P1(x1,y1)P2(x2,y2)我们就可以使用两点间距离公式 ,求点P的坐标.
,求点P的坐标.
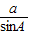 =
=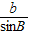 =
= =2R.
=2R. =
= ,
, ,即
,即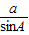 =2R,
=2R, =2R,
=2R,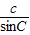 =2R,
=2R,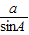 =
= =
=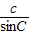 =2R,
=2R,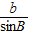 =2R,
=2R,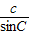 =2R”的证明过程,请你把“
=2R”的证明过程,请你把“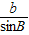 =2R”的证明过程补写出来.
=2R”的证明过程补写出来.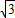 ,CA=
,CA=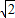 ,∠A=60°,求△ABC的外接圆半径R及∠C.
,∠A=60°,求△ABC的外接圆半径R及∠C.