题目内容
如图,四边形OABC是一张放在平面直角坐标系中的正方形纸片.点O与坐标原点重合,点A在x轴上,点C在y轴上,OC=4,点E为BC的中点,点N的坐标为(3,0),过点N且平行于y轴的直线MN与EB交于点M.现将纸片折叠,使顶点C落 在MN上,并与MN上的点G重合,折痕为EF,点F为折痕与y轴的交点.
在MN上,并与MN上的点G重合,折痕为EF,点F为折痕与y轴的交点.
(1)求点G的坐标;
(2)求折痕EF所在直线的解析式;
(3)设点P为直线EF上的点,是否存在这样的点P,使得以P,F,G为顶点的三角形为等腰三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
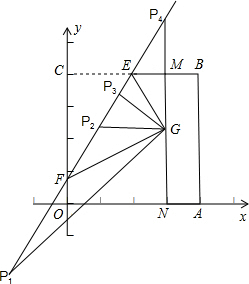 解:(1)∵四边形ABCO是正方形,
解:(1)∵四边形ABCO是正方形,∴BC=OA=4,
∵E为CB中点,
∴EB=2,
∵MN∥y轴,N(3,0),
∴MN⊥EB且MB=NA=1,
∴EM=1,
而EG=EC=2,
∴sin∠EGM=
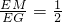 ,
,∴∠EGM=30°,
∴MG=EGcos30°=
 ,
,∴G(3,4-
 );
);(2)∵∠EGM=30°,
∴∠MEG=∠FEG=∠CEF=60°,
∴CF=CEtan60°=2
 ,
,∴FO=4-2
 ,
,∴F(0,4-2
 ),E(2,4),
),E(2,4),设直线EF的解析式:y=kx+b(k≠0),
∴
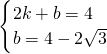 ,
,∴
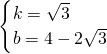 ,
,∴折痕EF所在直线解析式:y=
 x+4-2
x+4-2 ;
;(3)P1(-
 ,1-2
,1-2 ),P2(1,4-
),P2(1,4- ),P3(
),P3( ,7-2
,7-2 ),P4(3,4+
),P4(3,4+ ).
).分析:(1)根据正方形的性质,EB=2,根据MN∥y轴,N(3,0),MN⊥EB且MB=NA=1,可求EM=1,而EG=EC=2,所以sin∠EGM=
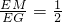 ,即∠EGM=30°,所以MG=EGcos30°=
,即∠EGM=30°,所以MG=EGcos30°= ,即G(3,4-
,即G(3,4- );
);(2)先求得F(0,4-2
 ),E(2,4),设直线EF的解析式:y=kx+b(k≠0),利用待定系数法可求得,折痕EF所在直线解析式:y=
),E(2,4),设直线EF的解析式:y=kx+b(k≠0),利用待定系数法可求得,折痕EF所在直线解析式:y= x+4-2
x+4-2 ;
;(3)分为以下几种情况:PF=FG,PF=PG,PG=FG,分别计算可得,P1(-
 ,1-2
,1-2 ),P2(1,4-
),P2(1,4- ),P3(
),P3( ,7-2
,7-2 ),P4(3,4+
),P4(3,4+ ).
).点评:主要考查了函数和几何图形的综合运用.解题的关键是会灵活的运用函数图象的性质和交点的意义求出相应的线段的长度或表示线段的长度,再结合具体图形的性质求解.

练习册系列答案
相关题目
 动.过点N作NP⊥OA于点P,连接AC交NP于Q,连接MQ.
动.过点N作NP⊥OA于点P,连接AC交NP于Q,连接MQ.  在MN上,并与MN上的点G重合,折痕为EF,点F为折痕与y轴的交点.
在MN上,并与MN上的点G重合,折痕为EF,点F为折痕与y轴的交点.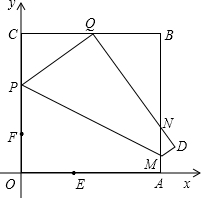
 (2012•呼伦贝尔)如图,四边形OABC是边长为2的正方形,反比例函数
(2012•呼伦贝尔)如图,四边形OABC是边长为2的正方形,反比例函数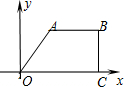 是( )
是( )