题目内容
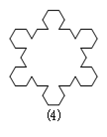
【题目】如图,第(1)个多边形由正三角形“扩展”而来,边数记为a3,第(2)个多边形由正方形“扩展”而来,边数记为a4,……,依此类推,由正n边形“扩展”而来的多边形的边数记为an(n≥3).则当an=90时,n的值是_________.



【答案】9
【解析】分析:第一个图形的边长是把正三角形的三边都减去1后,再加上2所得,第二个图形的边长是把正方形的四边都减去1后,再加上3所得,后面都是这个规律,由此列方程求解.
详解:由图可知中:
(1)a3=3(3-1+2)=12;
(2)a4=4(3-1+3)=20;
(3)a5=5(3-1+4)=30;
(4)a6=6(3-1+5)=42;
……
则an=n(3-1+n-1)=n(n+1).
所以n(n+1)=90,解得n=9或n=-10(舍).
故答案为9.

练习册系列答案
相关题目