题目内容
(2006•河南)如图,在平面直角坐标系中,直线y=- x+4分别交x轴、y轴于A、B两点.
x+4分别交x轴、y轴于A、B两点.(1)求两点的坐标;
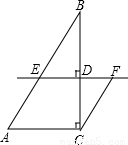
(2)设是直线AB上一动点(点P与点A不重合),设⊙P始终和x轴相切,和直线AB相交于C、D两点(点C的横坐标小于点D的横坐标)设P点的横坐标为m,试用含有m的代数式表示点C的横坐标;
(3)在(2)的条件下,若点C在线段AB上,求m为何值时,△BOC为等腰三角形?
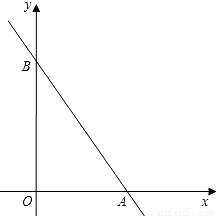
【答案】分析:(1)因为直线y=- x+4分别交x轴、y轴于A、B两点,所以分别令x=0、y=0,即可求出A、B的坐标;
x+4分别交x轴、y轴于A、B两点,所以分别令x=0、y=0,即可求出A、B的坐标;
(2)设点C的横坐标为n.由(1)知AB=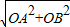 =5,所以sin∠OBA=
=5,所以sin∠OBA= ,要求点C的横坐标,可过C作CE⊥x轴于E,过P作PG⊥x轴于G,PF⊥CE于F,则∠FCP=∠OBA,PF=m-n.
,要求点C的横坐标,可过C作CE⊥x轴于E,过P作PG⊥x轴于G,PF⊥CE于F,则∠FCP=∠OBA,PF=m-n.
①若m<3时,因为P点的横坐标为m,P在直线y=- x+4上,所以PC=PG=-
x+4上,所以PC=PG=- m+4,利用三角函数可得PF=PC•sin∠FCP=PC•sin∠OBA,即可得到关于m、m的关系式,整理即可;
m+4,利用三角函数可得PF=PC•sin∠FCP=PC•sin∠OBA,即可得到关于m、m的关系式,整理即可;
②当m>3时,P在x轴的下方,所以PC=PG=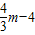 ,PF=PC•sin∠FCP=PC•sin∠OBA,整理即可得到另一个m、n的关系式;
,PF=PC•sin∠FCP=PC•sin∠OBA,整理即可得到另一个m、n的关系式;
(3)当点C在线段AB上时,由(2)知,C点的横坐标n= m-
m-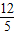 ,因为△BOC为等腰三角形,所以需要分情况讨论:
,因为△BOC为等腰三角形,所以需要分情况讨论:
①当CB=CO时,因为△OBA是直角三角形,∠BOA=90°,所以此时C为AB的中点,C点的横坐标为 ,即n=
,即n= ,即
,即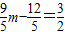 ,解之即可;
,解之即可;
②当CB=OB=4时,因为AB=5,可得AC=AB-CB=1,利用三角函数可得AE=AC•cos∠OAB= ,又因OE+AE=OA,就可得到关于m的方程,解之即可;
,又因OE+AE=OA,就可得到关于m的方程,解之即可;
③当OC=OB时,因为OB>OA,所以C在线段BA的延长线上,即在线段AB上不存在点C,使OC=OB.
解答:解:(1)当x=0时,y=4;当y=0时,- x+4=0,x=3.
x+4=0,x=3.
∴A(3,0),B(0,4).(2分)
(2)设点C的横坐标为n.由(1)知AB=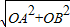 =5,
=5,
∴sin∠OBA= .
.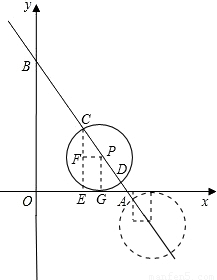
过C作CE⊥x轴于E,过P作PG⊥x轴于G,PF⊥CE于F,
则∠FCP=∠OBA,PF=m-n.
①当m<3时,∵PC=PG=- m+4,
m+4,
∴PF=PC•sin∠FCP=PC•sin∠OBA,
∴m-n=(- m+4)×
m+4)× .
.
解得n= m-
m-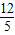 .(5分)
.(5分)
②当m>3时,PC=PG=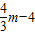 ,PF=PC•sin∠FCP=PC•sin∠OBA,
,PF=PC•sin∠FCP=PC•sin∠OBA,
∴m-n=( m-4)×
m-4)× .
.
解得n= m+
m+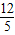 .(7分)
.(7分)
(3)当点C在线段AB上时,由(2)知,C点的横坐标n= m-
m-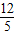 ,
,
以下两种情况△BOC为等腰三角形.
①当CB=CO时,
∵△OBA是直角三角形,∠BOA=90度.
∴此时C为AB的中点,
∴C点的横坐标为 .
.
∴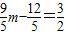 ,解得m=
,解得m=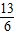 .(9分)
.(9分)
②当CB=OB时,
∵AB=5,
∴AC=AB-CB=1,
∴AE=AC•cos∠OAB= .
.
∵OE+AE=OA,
∴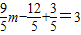 ,解得m=
,解得m= .
.
∵OB>OA,
∴在线段AB上不存在点C,使OC=OB.
所以,当m=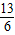 或m=
或m= 时,△BOC为等腰三角形.(11分)
时,△BOC为等腰三角形.(11分)
点评:本题的解决需要用到分类讨论、数形结合、方程和转化等数学思想方法.
 x+4分别交x轴、y轴于A、B两点,所以分别令x=0、y=0,即可求出A、B的坐标;
x+4分别交x轴、y轴于A、B两点,所以分别令x=0、y=0,即可求出A、B的坐标;(2)设点C的横坐标为n.由(1)知AB=
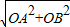 =5,所以sin∠OBA=
=5,所以sin∠OBA= ,要求点C的横坐标,可过C作CE⊥x轴于E,过P作PG⊥x轴于G,PF⊥CE于F,则∠FCP=∠OBA,PF=m-n.
,要求点C的横坐标,可过C作CE⊥x轴于E,过P作PG⊥x轴于G,PF⊥CE于F,则∠FCP=∠OBA,PF=m-n.①若m<3时,因为P点的横坐标为m,P在直线y=-
 x+4上,所以PC=PG=-
x+4上,所以PC=PG=- m+4,利用三角函数可得PF=PC•sin∠FCP=PC•sin∠OBA,即可得到关于m、m的关系式,整理即可;
m+4,利用三角函数可得PF=PC•sin∠FCP=PC•sin∠OBA,即可得到关于m、m的关系式,整理即可;②当m>3时,P在x轴的下方,所以PC=PG=
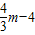 ,PF=PC•sin∠FCP=PC•sin∠OBA,整理即可得到另一个m、n的关系式;
,PF=PC•sin∠FCP=PC•sin∠OBA,整理即可得到另一个m、n的关系式;(3)当点C在线段AB上时,由(2)知,C点的横坐标n=
 m-
m-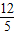 ,因为△BOC为等腰三角形,所以需要分情况讨论:
,因为△BOC为等腰三角形,所以需要分情况讨论:①当CB=CO时,因为△OBA是直角三角形,∠BOA=90°,所以此时C为AB的中点,C点的横坐标为
 ,即n=
,即n= ,即
,即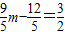 ,解之即可;
,解之即可;②当CB=OB=4时,因为AB=5,可得AC=AB-CB=1,利用三角函数可得AE=AC•cos∠OAB=
 ,又因OE+AE=OA,就可得到关于m的方程,解之即可;
,又因OE+AE=OA,就可得到关于m的方程,解之即可;③当OC=OB时,因为OB>OA,所以C在线段BA的延长线上,即在线段AB上不存在点C,使OC=OB.
解答:解:(1)当x=0时,y=4;当y=0时,-
 x+4=0,x=3.
x+4=0,x=3.∴A(3,0),B(0,4).(2分)
(2)设点C的横坐标为n.由(1)知AB=
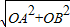 =5,
=5,∴sin∠OBA=
 .
.
过C作CE⊥x轴于E,过P作PG⊥x轴于G,PF⊥CE于F,
则∠FCP=∠OBA,PF=m-n.
①当m<3时,∵PC=PG=-
 m+4,
m+4,∴PF=PC•sin∠FCP=PC•sin∠OBA,
∴m-n=(-
 m+4)×
m+4)× .
.解得n=
 m-
m-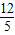 .(5分)
.(5分)②当m>3时,PC=PG=
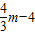 ,PF=PC•sin∠FCP=PC•sin∠OBA,
,PF=PC•sin∠FCP=PC•sin∠OBA,∴m-n=(
 m-4)×
m-4)× .
.解得n=
 m+
m+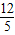 .(7分)
.(7分)(3)当点C在线段AB上时,由(2)知,C点的横坐标n=
 m-
m-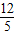 ,
,以下两种情况△BOC为等腰三角形.
①当CB=CO时,
∵△OBA是直角三角形,∠BOA=90度.
∴此时C为AB的中点,
∴C点的横坐标为
 .
.∴
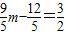 ,解得m=
,解得m=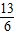 .(9分)
.(9分)②当CB=OB时,
∵AB=5,
∴AC=AB-CB=1,
∴AE=AC•cos∠OAB=
 .
.∵OE+AE=OA,
∴
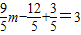 ,解得m=
,解得m= .
.∵OB>OA,
∴在线段AB上不存在点C,使OC=OB.
所以,当m=
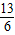 或m=
或m= 时,△BOC为等腰三角形.(11分)
时,△BOC为等腰三角形.(11分)点评:本题的解决需要用到分类讨论、数形结合、方程和转化等数学思想方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
(2006•河南)如图,∠AOB=45°,过OA上到点O的距离分别为1,2,3,4,5 …的点作OA的垂线与OB相交,再按一定规律标出一组如图所示的黑色梯形.设前n个黑色梯形的面积和为Sn.
(1)请完成上面的表格;
(2)已知Sn与n之间满足一个二次函数关系,试求出这个二次函数的解析式.

| n | 1 | 2 | 3 | … |
| Sn | … |
(2)已知Sn与n之间满足一个二次函数关系,试求出这个二次函数的解析式.

(2006•河南)如图,∠AOB=45°,过OA上到点O的距离分别为1,2,3,4,5 …的点作OA的垂线与OB相交,再按一定规律标出一组如图所示的黑色梯形.设前n个黑色梯形的面积和为Sn.
(1)请完成上面的表格;
(2)已知Sn与n之间满足一个二次函数关系,试求出这个二次函数的解析式.

| n | 1 | 2 | 3 | … |
| Sn | … |
(2)已知Sn与n之间满足一个二次函数关系,试求出这个二次函数的解析式.