题目内容
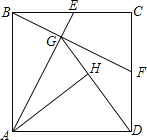
【题目】正方形ABCD中,E点为BC中点,连接AE,过B点作BF⊥AE,交CD于F点,交AE于G点,
连接GD,过A点作AH⊥GD交GD于H点.
(1)求证:△ABE≌△BCF;
(2)若正方形边长为4,AH=![]() ,求△AGD的面积.
,求△AGD的面积.
【答案】(1)、答案见解析;(2)、![]()
【解析】
试题分析:(1)、根据正方形的性质得出∠1+∠2=90°,根据AE⊥BF得出∠3+∠2=90°,从而说明∠1=∠3,根据正方形得出∠ABE=∠BCF=90°,AB=BC,从而得出三角形全等;(2)、延长BF交AD延长线于M点,根据全等得出CF=BE,根据中点的性质得出CF=![]() CD=FD,从而得出△BCF和△MDF全等,根据正方形的性质得出GD和AH的长度,从而得出面积.
CD=FD,从而得出△BCF和△MDF全等,根据正方形的性质得出GD和AH的长度,从而得出面积.
试题解析:(1)、正方形ABCD中,∠ABE=90°,
∴∠1+∠2=90°,
又AE⊥BF,
∴∠3+∠2=90°,
则∠1=∠3
又∵四边形ABCD为正方形,
∴∠ABE=∠BCF=90°,AB=BC
在△ABE和△BCF中,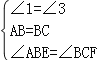
∴△ABE≌△BCF(ASA)
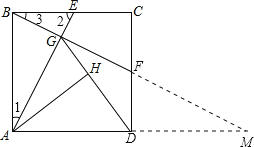
(2)、延长BF交AD延长线于M点, ∴∠MDF=90°
由(1)知△ABE≌△BCF, ∴CF=BE
∵E点是BC中点, ∴BE=![]() BC,即CF=
BC,即CF=![]() CD=FD,
CD=FD,
在△BCF和△MDF中,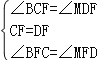
∴△BCF≌△MDF(ASA)
∴BC=DM,即DM=AD,D是AM中点
又AG⊥GM,即△AGM为直角三角形,
∴GD=![]() AM=AD
AM=AD
又∵正方形边长为4,
∴GD=4
S△AGD=![]() GDAH=
GDAH=![]() ×4×
×4×![]() =
=![]() .
.

练习册系列答案
相关题目