��Ŀ����
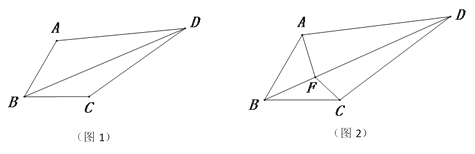
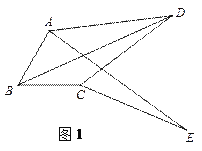
����Ŀ����ͼ1�����ı���ABCD�У�BA=BC����ABC=60�㣬��ADC=30�㣬���ӶԽ���BD��
��1�����߶�CD�Ƶ�C˳ʱ����ת60��õ��߶�CE������AE��
�������ⲹȫͼ1��
�����ж�AE��BD��������ϵ����֤����Ľ��ۣ�
��2���ڣ�1���������£�ֱ��д���߶�DA��DB��DC֮���������ϵ��
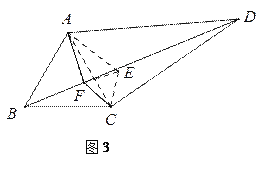
��3����ͼ2��F�ǶԽ���BD��һ�㣬�������AFC=150�㣬����FA��FC��̽���߶�FA��FB��FC֮���������ϵ����֤����
���𰸡���1����ͼ�μ�������AE=BD��2���жϣ� ![]() ��3���ж�
��3���ж�![]() ��֤��������
��֤��������
�������������������1���ٸ������⻭ͼ���ɣ�
������AC��֤����BCD�ա�ACE���ɣ�
��2������DE����֤������ADEΪֱ�������Σ��ɹ��ɶ������ɵó����ۣ�
��3�����߶�CF�Ƶ�C˳ʱ����ת60��õ��߶�CE������EF��EA��֤����BCD�ա�ACE��ֱ��������AEF����Ϲ��ɶ�������֤��.
�����������1���ٲ�ȫͼ��,��ͼ1
���ж�: AE=BD
֤������ͼ2������AC����BA=BC���ҡ�ABC=60�� ���ABC�ǵȱ�������
���ACB=60�㣬��CA=CB�߽��߶�CD�Ƶ�C˳ʱ����ת60��õ��߶�CE ��CD=CE���ҡ�DCE=60��
���BCD=��ACE
���BCD�ա�ACE��SAS�� ��AE=BD

��2���жϣ� ![]()
��3���жϣ� ![]()
֤������ͼ3,����AC����BA=BC���ҡ�ABC=60��
���ABC�ǵȱ������Σ����ACB=60�㣬��CA=CB
���߶�CF�Ƶ�C˳ʱ����ת60��õ��߶�CE������EF��EA
��CE=CF���ҡ�FCE=60�㣬���CEF�ǵȱ�������
���CFE=60�㣬��FE=FC�����BCF=��ACE
���BCF�ա�ACE��SAS������AE=BF
�ߡ�AFC=150��, ��CFE=60�㣬���AFE=90��
��Rt��AEF�� �� ![]()
��![]() .
.