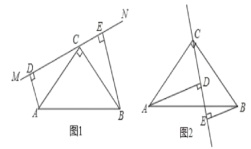
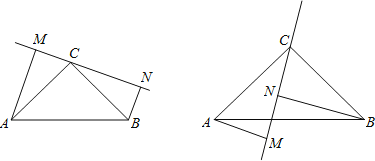
ЬтФПФкШн
ЁОЬтФПЁПдквЛДЮЁАЙЙдьЙДЙЩЪ§ЁБЕФЬНОПадбЇЯАжаЃЌРЯЪІИјГіСЫЯТБэЃК

ЦфжаmЁЂnЮЊе§ећЪ§ЃЌЧвm>n.
(1)ЙлВьБэИёЃЌЕБm=2ЃЌn=1ЪБЃЌДЫЪБЖдгІЕФaЁЂbЁЂcЕФжЕФмЗёЮЊжБНЧШ§НЧаЮШ§БпЕФГЄ?ЫЕУїФуЕФРэгЩЃЎ
(2)ЬНОПaЃЌbЃЌcгыmЁЂnжЎМфЕФЙиЯЕВЂгУКЌmЁЂnЕФДњЪ§ЪНБэЪОЃКa=___ЃЌb=___ЃЌc=___.
(3)вдaЃЌbЃЌcЮЊБпГЄЕФШ§НЧаЮЪЧЗёвЛЖЈЮЊжБНЧШ§НЧаЮ?ШчЙћЪЧЃЌЧыЫЕУїРэгЩЃЛШчЙћВЛЪЧЃЌЧыОйГіЗДР§.
ЁОД№АИЁПЃЈ1ЃЉФмЃЌРэгЩМћНтЮіЃЛЃЈ2ЃЉm2+n2ЃЌ2mnЃЌm2-n2ЃЛЃЈ3ЃЉвЛЖЈЃЌРэгЩМћНтЮі.
ЁОНтЮіЁП
ЃЈ1ЃЉМЦЫуГіaЁЂbЁЂcЕФжЕЃЌИљОнЙДЙЩЖЈРэЕФФцЖЈРэМДПЩХаЖЯЃЛ
ЃЈ2ЃЉИљОнИјГіЕФЪ§ОнзмНсМДПЩЃЛ
ЃЈ3ЃЉЗжБ№МЦЫуГіa2ЁЂb2ЁЂc2ЃЌИљОнЙДЙЩЖЈРэЕФФцЖЈРэНјааХаЖЯЃЎ
НтЃКЃЈ1ЃЉЕБm=2ЃЌn=1ЪБЃЌa=5ЁЂb=4ЁЂc=3ЃЌ
Ёп32+42=52ЃЌ
ЁрaЁЂbЁЂcЕФжЕФмЮЊжБНЧШ§НЧаЮШ§БпЕФГЄЃЛ
ЃЈ2ЃЉЙлВьЕУЃЌa=m2+n2ЃЌb=2mnЃЌc=m2-n2ЃЛ
ЃЈ3ЃЉвдaЃЌbЃЌcЮЊБпГЄЕФШ§НЧаЮвЛЖЈЮЊжБНЧШ§НЧаЮЃЌ
Ёпa2=ЃЈm2+n2ЃЉ2=m4+2m2n2+n4ЃЌ
b2+c2=m4-2m2n2+n4+4m2n2=m4+2m2n2+n4ЃЌ
Ёрa2=b2+c2ЃЌ
ЁрвдaЃЌbЃЌcЮЊБпГЄЕФШ§НЧаЮвЛЖЈЮЊжБНЧШ§НЧаЮЃЎ

ЁОЬтФПЁПФГЗчОАЧјЖд![]() ИіТУгЮОАЕуЕФгЮПЭШЫЪ§НјааСЫЭГМЦЃЌгаЙиЪ§ОнШчЯТБэЃК
ИіТУгЮОАЕуЕФгЮПЭШЫЪ§НјааСЫЭГМЦЃЌгаЙиЪ§ОнШчЯТБэЃК
ОАЕу |
|
|
|
|
|
ЦБМлЃЈдЊЃЉ |
|
|
|
|
|
ЦНОљШеШЫЪ§ЃЈЧЇШЫЃЉ |
|
|
|
|
|
![]() ШчЙћетИіаЧЦкЬьФуШЅДЫЗчОАЧјгЮЭцЃЌаЁИеЁЂаЁУївВШЅСЫЃЌФудкФФИіОАЕугіМћЫћУЧСНИіЕФЛњЛсНЯДѓЃПЮЊЪВУДЃП
ШчЙћетИіаЧЦкЬьФуШЅДЫЗчОАЧјгЮЭцЃЌаЁИеЁЂаЁУївВШЅСЫЃЌФудкФФИіОАЕугіМћЫћУЧСНИіЕФЛњЛсНЯДѓЃПЮЊЪВУДЃП
![]() ШчЙћЕНСЫетИіЗчОАЧјЃЌФуВЛЯыАбетМИИіОАЕуШЋВПВЮЙлЭъЃЌЕЋгжВЛжЊбЁФФвЛИіЃЌгкЪЧФуЯыГівЛИіжївтЃКзЅуЮЃЌФЧУДЃЌФузЅГіФФжжЦБМлЕФЛњЛсНЯДѓгаЖрДѓЃПДЫЪБФуВЮЙлФФИіОАЕуЕФЛњЛсНЯДѓЃП
ШчЙћЕНСЫетИіЗчОАЧјЃЌФуВЛЯыАбетМИИіОАЕуШЋВПВЮЙлЭъЃЌЕЋгжВЛжЊбЁФФвЛИіЃЌгкЪЧФуЯыГівЛИіжївтЃКзЅуЮЃЌФЧУДЃЌФузЅГіФФжжЦБМлЕФЛњЛсНЯДѓгаЖрДѓЃПДЫЪБФуВЮЙлФФИіОАЕуЕФЛњЛсНЯДѓЃП