题目内容
【题目】如图,正方形纸片![]() ,
,![]() 为正方形
为正方形![]() 边上的一点(不与点
边上的一点(不与点![]() ,点
,点![]() 重合).将正方形纸片折叠,使点
重合).将正方形纸片折叠,使点![]() 落在点
落在点![]() 处,点
处,点![]() 落在点
落在点![]() 处,
处,![]() 交
交![]() 于点
于点![]() ,折痕为
,折痕为![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() 平分
平分![]() ;④
;④![]() ;⑤
;⑤![]() ,其中正确结论的个数是( )
,其中正确结论的个数是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
①③利用正方形的性质、翻折不变性即可解决问题;
②构造全等三角形即可解决问题;
④如图2,过B作BQ⊥PH,垂足为Q.证明△ABP≌△QBP(AAS),以及△BCH≌△BQH即可判断;
⑤利用特殊位置,判定结论即可;
解:根据翻折不变性可知:PE=BE,故①正确;
∴∠EBP=∠EPB.
又∵∠EPH=∠EBC=90°,
∴∠EPH∠EPB=∠EBC∠EBP.
即∠PBC=∠BPH.
又∵AD∥BC,
∴∠APB=∠PBC.
∴∠APB=∠BPH,即![]() 平分
平分![]() ,故③正确;
,故③正确;
如图1中,作FK⊥AB于K.设EF交BP于O.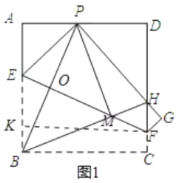
∵∠FKB=∠KBC=∠C=90°,
∴四边形BCFK是矩形,
∴KF=BC=AB,
∵EF⊥PB,
∴∠BOE=90°,
∵∠ABP+∠BEO=90°,∠BEO+∠EFK=90°,
∴∠ABP=∠EFK,
∵∠A=∠EKF=90°,
∴△ABP≌△KFE(ASA),
∴EF=BP,故②正确,
如图2,过B作BQ⊥PH,垂足为Q.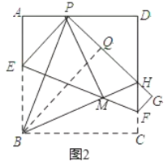
由(1)知∠APB=∠BPH,
在△ABP和△QBP中,
∠APB=∠BPH,∠A=∠BQP,BP=BP,
∴△ABP≌△QBP(AAS).
∴AP=QP,AB=BQ.
又∵AB=BC,
∴BC=BQ.
又∵∠C=∠BQH=90°,BH=BH,
∴△BCH≌△BQH(HL)
∴QH=HC,
∴PH=PQ+QH=AP+HC,故④正确;
当点P与A重合时,显然MH>MF,故⑤错误,
故选:B.

 名校课堂系列答案
名校课堂系列答案【题目】已知抛物线y=(x﹣1)2﹣1.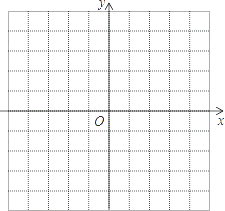
(1)该抛物线的对称轴是 , 顶点坐标;
(2)选取适当的数据填入下表,并在图中的直角坐标系内描点画出该抛物线的图象;
x | … | … | |||||
y | … | … |
(3)根据图象,直接写出当y<0时,x的取值范围.
【题目】中华文明,源远流长;中华汉字,寓意深广,为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好地了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
成绩x/分 | 频数 | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | 40 | n |
80≤x<90 | m | 0.35 |
90≤x≤100 | 50 | 0.25 |
请根据所给信息,解答下列问题:
(1)m= ,n= ;
(2)请补全频数分布直方图;
(3)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等约有多少人?




