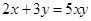题目内容
因式分解(每题5分,共计30分)
小题1:(1)
小题2:(2)
小题3:(3)
小题4:(4)


小题5:(5)
小题6:(6)
小题1:(1)

小题2:(2)

小题3:(3)

小题4:(4)



小题5:(5)

小题6:(6)

小题1:解:原式

小题2:

小题3:解:原式

小题4:

小题5:解:原式

小题6:解:原式=

分析:(1)首先提取公因式x,再用平方差公式进行二次分解即可;
(2)利用完全平方公式直接分解;
(3)首先提取负号,再提取公因式3m,最后利用完全平方公式进行二次分解即可;
(4)直接利用完全平方公式分解;
(5)首先把原式变为=9x2(a-b)-y2(a-b),再提取公因式a-b,最后利用平方差公式进行二次分解即可;
(6)直接利用十字相乘法进行分解因式.
解:(1)原式=x(x2-25)=x(x+5)(x-5);
(2)原式=(x+2)2;
(3)原式=-3m(n2-4n+4)=-3m(n-2)2;
(4)原式=[(x2-6)-3]2=(x2-9)2=(x+3)2(x-3)2;
(5)原式=9x2(a-b)-y2(a-b)=(a-b)(9x2-y2)=(a-b)(3x+y)(3x-y);
(6)原式=(y-5)(y+4).
点评:此题主要考查了提公因式法分解因式与公式法分解因式,以及十字相乘法分解因式的综合运用,关键是注意观察式子的特点找准分解方法,注意分解要彻底.
(2)利用完全平方公式直接分解;
(3)首先提取负号,再提取公因式3m,最后利用完全平方公式进行二次分解即可;
(4)直接利用完全平方公式分解;
(5)首先把原式变为=9x2(a-b)-y2(a-b),再提取公因式a-b,最后利用平方差公式进行二次分解即可;
(6)直接利用十字相乘法进行分解因式.
解:(1)原式=x(x2-25)=x(x+5)(x-5);
(2)原式=(x+2)2;
(3)原式=-3m(n2-4n+4)=-3m(n-2)2;
(4)原式=[(x2-6)-3]2=(x2-9)2=(x+3)2(x-3)2;
(5)原式=9x2(a-b)-y2(a-b)=(a-b)(9x2-y2)=(a-b)(3x+y)(3x-y);
(6)原式=(y-5)(y+4).
点评:此题主要考查了提公因式法分解因式与公式法分解因式,以及十字相乘法分解因式的综合运用,关键是注意观察式子的特点找准分解方法,注意分解要彻底.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 、
、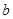 ,高线长恰好等于圆的直径
,高线长恰好等于圆的直径 ,
,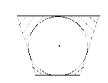




 与
与 的和仍然是一个单项式,则m、n的值是( )
的和仍然是一个单项式,则m、n的值是( ) ,
,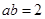 ,则
,则 ___________
___________