��Ŀ����
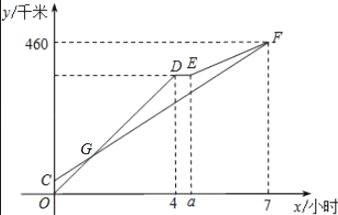
����Ŀ���ס���������A�س�����ͬһ·��ʻ��B�أ��׳��ȳ�������ʻ��B�أ�40���Ӻ��ҳ�������������ʻһ��ʱ�����;�еĻ�վװ����ʱ��Сʱ���������ػ��Ϊ����ʻ��ȫ���ٶȼ�����50ǧ��/ʱ�������׳�ͬʱ����B�أ�����������A�ص�·��y��ǧ�ף����ҳ���ʻʱ��x��Сʱ��֮��ĺ���ͼ����ͼ��ʾ��
����ͼ����Ϣ����������⣺
��1��ֱ��д��a��ֵ������׳����ٶȣ�
��2����ͼ���߶�EF����ʾ��y��x�ĺ�����ϵʽ����ֱ��д���Ա���x��ȡֵ��Χ��
��3���ҳ���������Сʱ��׳����15ǧ�ף�ֱ��д���𰸣�
���𰸡���1��4.5��60��2��y=40x+180��4.5��x��7����3��![]() Сʱ��
Сʱ��![]() Сʱ��
Сʱ��![]() Сʱ
Сʱ
���������⣺��1��a=4.5��
�׳����ٶ�=![]() =60��ǧ��/Сʱ����
=60��ǧ��/Сʱ����
��2�����ҿ�ʼ���ٶ�Ϊvǧ��/Сʱ��
��4v+��7��4.5����v��50��=460�����v=90��ǧ��/Сʱ����
4v=360��
��D��4��360����E��4.5��360����
��ֱ��EF�Ľ���ʽΪy=kx+b��
��E��4.5��360����F��7��460�������![]() ��
��
���![]() ��
��
�����߶�EF����ʾ��y��x�ĺ�����ϵʽΪy=40x+180��4.5��x��7����
��3���׳�ǰ40���ӵ�·��Ϊ60��![]() =40ǧ�ף���C��0��40����
=40ǧ�ף���C��0��40����
��ֱ��CF�Ľ���ʽΪy=mx+n��
��C��0��40����F��7��460�������![]() �����
�����![]() ��
��
����ֱ��CF�Ľ���ʽΪy=60x+40��
��ֱ��OD�Ľ���ʽΪy=90x��0��x��4����
�����������;������ΪG����60x+40=90x�����x=![]() Сʱ�����ҳ�����
Сʱ�����ҳ�����![]() Сʱ��������������
Сʱ��������������
���ҳ���OG��ʱ����60x+40��90x=15�����x=![]() ������0��
������0��![]() Сʱ֮�䣬�������⣻
Сʱ֮�䣬�������⣻
���ҳ���GD��ʱ����90x����60x+40��=15�����x=![]() ������
������![]() ��4Сʱ֮�䣬�������⣻
��4Сʱ֮�䣬�������⣻
���ҳ���DE��ʱ����360����60x+40��=15�����x=![]() ��������4��4.5֮�䣬���������⣻
��������4��4.5֮�䣬���������⣻
���ҳ���EF��ʱ����40x+180����60x+40��=15�����x=![]() ������4.5��7֮�䣬�������⣮
������4.5��7֮�䣬�������⣮
�����ҳ�����![]() Сʱ��
Сʱ��![]() Сʱ��
Сʱ��![]() Сʱ������׳����15ǧ�ף�
Сʱ������׳����15ǧ�ף�

 �Űٷֿ�ʱ����ϵ�д�
�Űٷֿ�ʱ����ϵ�д� ������״Ԫ��ҵϵ�д�
������״Ԫ��ҵϵ�д� ��ʱ�ƿ�������ϰϵ�д�
��ʱ�ƿ�������ϰϵ�д�

