Question

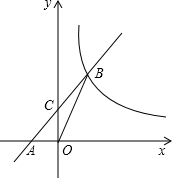（2012•邯郸二模）已知：如图，在平面直角坐标系xOy中，直线AB与x轴交于点A（-4，0），与反比例函数在第一象限内的图象的交于点B，在第一象限内，当一次函数值大于反比例函数值时，则x＞4，连接BO，若S_△AOB=8．
（1）求该反比例函数的解析式和直线AB的解析式；
（2）若直线AB与y轴的交点为C，求△OCB的面积．

Answer 1

分析：（1）根据在第一象限内，当一次函数值大于反比例函数值时，则x＞4得出点B横坐标为4，设点B的坐标为（4，n），根据S_△AOB=8，OA=4，求出点B的坐标，设该反比例函数的解析式为y=

k

x

（k≠0）则k=16，根据直线AB经过点A和点B，运用待定系数法即可求出直线AB的解析式；
（2）根据直线AB的解析式求出点C的坐标，再根据点B的横坐标即可求出△OCB的面积．

解答：（1）解：∵直线AB与反比例函数在第一象限内的图象的交于点B，在第一象限内，当一次函数值大于反比例函数值时，则x＞4，
∴点B横坐标为4，
设点B的坐标为（4，n），
∵S_△AOB=8，OA=4，
∴

1

2

×4n=8，
解n=4，
设该反比例函数的解析式为y=

k

x

（k≠0）
∵反比例函数在第一象限内的图象经过点B（4，4），
∴k=16，
设直线AB的解析式为y=ax+b（a≠0）
∵直线AB经过点A（-4，0），点B（4，4），
∴

-4a+b=0 4a+b=4

，
解得：

a= 1 2 b=2

，
∴该反比例函数的解析式为y=

16

x

，直线AB的解析式为y=

1

2

x+2；         

（2）在y=

1

2

x+2中，令x=0，得y=2，
则点C的坐标是（0，2），
OC=2，
则S_△OCB=

1

2

×OC×|点B的横坐标|=

1

2

×2×4=4．

点评：本题考查反比例函数和一次函数的交点问题，关键是根据函数的图象求出点B的横坐标，用到的知识点是函数的解析式的求法，三角形的面积求法．