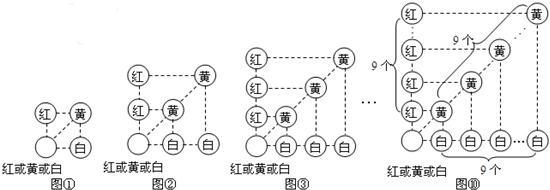
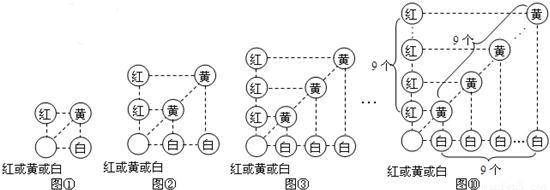
题目内容
在不透明的口袋中装有除颜色不同外,其他都相同的5个球,其中红球3个,黑球1个,白球1个,每次从袋中摸出1个球记录球色后仍放入袋中,并充分搅匀再摸.
(1)请你先观察表1,摸球实验的次数要求从20次~600次,先想一想,采取什么办法才能在不太长的时间内完成这样大次数的实验?
(2)根据实验得到的数据完成表1.
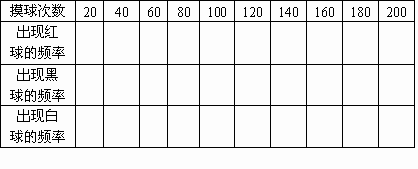
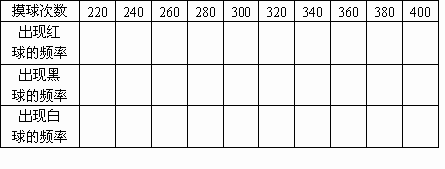
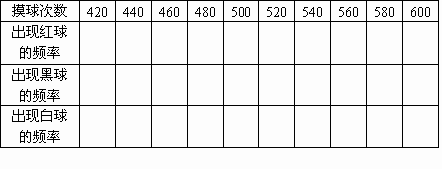
(3)根据表中所填的数据分别绘制红球和白球的频率折线统计图.
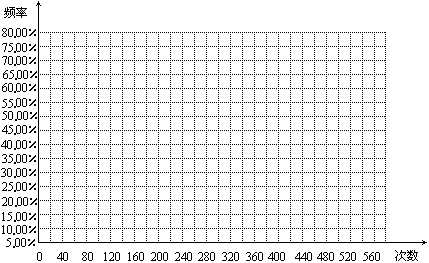
(4)通过分析图表1中的数据和折线统计图,你发现了些什么?
答案:
解析:
解析:
|
(4)摸到红球、黑球或白球,是一个不确定事件,但这种不确定事件并非完全没有规律可循,可采用大次数实验,随着实验次数的不断增加,这种事件发生的频率趋于一个稳定的数值,我们就可用这个较平稳的数值,来估计不确定事件发生的机会的大小.比如在这个摸球实验中,我们可以估计一次摸球,摸到红球的机会是60%,摸到黑球和白球的机会均是20%左右. |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列说法中正确的是( )
| A、抛掷质地均匀的硬币100次,必然有50次正面朝上 | B、在不透明的口袋中装有1只红球、5只白球(除颜色外其余都相同)搅匀后从中任意摸出一个球,摸出的一定是白球 | C、抛掷一枚质地均匀的骰子,朝上的点数为奇数与朝上的点数为偶数的概率相等 | D、某种福利彩票中奖的概率是1%,买100张该种彩票一定能中奖 |