题目内容
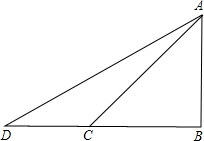如图，为了测量旗杆的高度，小王在离旗杆9米处的点C测得旗杆顶端A的仰角为50°；小李从C点向后退了7米到D点（B，C，D在同一直线上），量得旗杆顶端A的仰角为40度．根据这些数据，小王和小李能否求出旗杆的高度？若能，请写出求解过程；若不能，请说明理由．
分析：首先分析图形：根据题意构造直角三角形；本题涉及到两个直角三角形△ADB、△ABC，应利用其公共边AB构造等量关系，借助CD=DB-DC=7，BC=9构造方程关系式，进而可求出答案．
解答：解：能求出旗杆的高度．
根据题意可知，在△ABC中，∠ACB=50°，∠B=90°则∠BAC=40°，
在△ABC与△DBA中，
∠BAC=40°=∠D，∠B=∠B，
∴△ABC∽△DBA．
∴
=
．
又∵BC=9，DB=7+9=16，
∴AB2=9×16．
∴AB=12（m）．
即旗杆的高度为12米．
根据题意可知，在△ABC中，∠ACB=50°，∠B=90°则∠BAC=40°，
在△ABC与△DBA中，
∠BAC=40°=∠D，∠B=∠B，
∴△ABC∽△DBA．
∴
| AB |
| BC |
| DB |
| AB |
又∵BC=9，DB=7+9=16，
∴AB2=9×16．
∴AB=12（m）．
即旗杆的高度为12米．
点评：本题要求学生借助仰角关系构造直角三角形，并结合图形利用三角函数解直角三角形．
练习册系列答案
相关题目
如图，为了测量笔直的旗杆AB的高度，现将高度为1米的测角仪CD（即CD=1米）与旗杆AB置于同一水平面上，且与旗杆底部相距15米（即CB=15米），测得旗杆顶端A的仰角∠ADE=30°，求旗杆AB的高度．（结果保留根号）
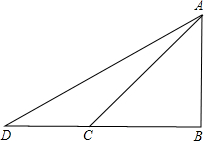如图，为了测量旗杆的高度，小王在离旗杆9米处的点C测得旗杆顶端A的仰角为50°；小李从C点向后退了7米到D点（B，C，D在同一直线上），量得旗杆顶端A的仰角为40度．根据这些数据，小王和小李能否求出旗杆的高度？若能，请写出求解过程；若不能，请说明理由．
如图，为了测量笔直的旗杆AB的高度，现将高度为1米的测角仪CD（即CD=1米）与旗杆AB置于同一水平面上，且与旗杆底部相距15米（即CB=15米），测得旗杆顶端A的仰角∠ADE=30°，求旗杆AB的高度．（结果保留根号）