题目内容
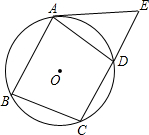（1997•海南）如图，已知⊙O是梯形ABCD的外接圆，DC∥AB，过A点作⊙O的切线交CD的延长线于E．求证：AD2=DE•AB．分析：连接AC，因为AB∥CD，所以∠1=∠2，由圆的内接四边形定理可证明∠ADE=∠B，进而证明△ABC∽△ADE，所以AD：AB=DE：BC．因为AB、CD是⊙O中的平行弦，所以BC=AD，所以AD2=DE•AB．
解答：证明：连接AC，
∵AB∥CD，
∴∠1=∠2，
又∵AE是⊙O的切线，
∴∠2=∠3，
∴∠1=∠3，
而∠ADE是四边形ABCD的外角，
∴∠ADE=∠B，
∴△ABC∽△ADE．
∴AD：AB=DE：BC．
∵AB、CD是⊙O中的平行弦，
∴BC=AD，
∴AD2=DE•AB．
∵AB∥CD，
∴∠1=∠2，
又∵AE是⊙O的切线，
∴∠2=∠3，
∴∠1=∠3，
而∠ADE是四边形ABCD的外角，
∴∠ADE=∠B，
∴△ABC∽△ADE．
∴AD：AB=DE：BC．
∵AB、CD是⊙O中的平行弦，
∴BC=AD，
∴AD2=DE•AB．
点评：本题利用了圆周角定理，垂径定理的运用，以及平行线的性质和相似三角形的判定和性质．
练习册系列答案
口算能手系列答案
相关题目
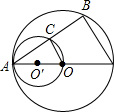（1997•海南）如图，⊙O与⊙O′内切于A，⊙O′过O点，⊙O的弦AB交⊙O′于C．若⊙O的半径为13cm，AB的长为24cm，则OC的长为
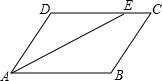（1997•海南）如图，在?ABCD中，∠A的平分线交DC于E．若DE：EC=3：1，AB的长为8，求AD的长．
（1997•海南）如图，正三角ABC内接于⊙O，已知⊙O的半径为2cm，求阴影部分的面积（精确到0.1cm）．[可供选用的数据：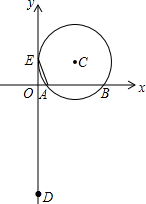
（1997•海南）如图，在直角坐标系xOy中，点A、B在x轴上，以AB为弦的⊙O与y轴相切于E点，E点的坐标为（0，2），AE的长为