题目内容
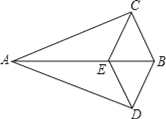
【题目】如图,在平行四边形ABCD中,E、F分别是边AD、BC的中点,AC分别交BE、DF于点M、N.给出下列结论:①△ABM≌△CDN;②AM=![]() AC;③DN=2NF;④S△AMB=
AC;③DN=2NF;④S△AMB=![]() △ABC;其中正确的结论是______________(只填序号)。
△ABC;其中正确的结论是______________(只填序号)。

【答案】①②③.
【解析】
本题先结合平行四边形性质,根据ASA得出△ABM≌△CDN,从而得出DN=BM,AM=CN;再由三角形中位线得出CN=MN,BM=DN=2NF,同时S![]() =
=![]() S
S![]() .
.
∵因为平行四边形ABCD,
∴AD=BC,AB=CD,且AD∥BC,AB∥CD∠BAE=∠DCF,
∵E、F分别是边AD、BC的中点,
∴AE=DE=BF=CF,
∴四边形BFDE是平行四边形
∴BE∥DF,
在△ABE和△CDF中
∵ ,
,
∴△ABE≌△CDF(SAS),
∴∠ABM=∠CDN,
∵AB∥CD,
∴∠BAM=∠DCN,
在△ABM和△CDN中
∵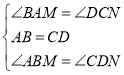 ,
,
∴△ABM≌△CDN(ASA),∴①正确;
∵E是AD的中点,BE∥DF,
∴M是AN的中点,
同理N是CM的中点,
∴AM=![]() AC,故②正确;
AC,故②正确;
∵F为BC的中点,
∴NF为三角形BCM的中位线,
∴BM=2NF
∴DN=2NF,故③正确;
∵CN=MN=AM,
∴S![]() =
=![]() S
S![]() ,故④不正确,
,故④不正确,
∴其中正确的结论是①②③.
故答案为:①②③.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目