题目内容
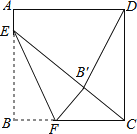
【题目】如图,点D,E分别是⊙O的内接正三角形ABC的AB,AC边上的中点,若⊙O的半径为2,则DE的长等于( )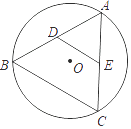
A.![]()
B.![]()
C.1
D.![]()
【答案】A
【解析】解:连接BO并延长交⊙O于F,连接CF,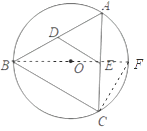
则BF为⊙O的直径,
∴∠BCF=90°,
∵△ABC是等边三角形,
∴∠A=60°,
∴∠F=∠A=60°,
∵⊙O的半径为2,
∴BF=4,
∴BC=2 ![]() ,
,
∵点D、E分别是AB、AC边上的中点,
∴DE= ![]() BC=
BC= ![]() ,
,
故答案为:A.
根据题意可作辅助线,连接BO并延长交⊙O于F,连接CF,由直径所对的圆周角是直角可得∠BCF=90°,由已知条件可得∠A=60°,根据在同圆或等圆中,同弧所对的圆周角相等可得∠F=∠A,在直角三角形BCF中,用勾股定理或锐角三角函数可求BC的长,根据三角形的中位线定理可得DE= ![]() BC。所以选项A符合题意。
BC。所以选项A符合题意。

练习册系列答案
相关题目