题目内容
【题目】如图，在平面直角坐标系中，直线AB和抛物线交于点A（-4，0），B（0，4），且点B是抛物线的顶点．
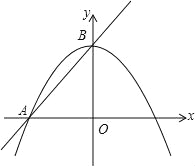
（1）求直线AB和抛物线的解析式．
（2）点P是直线上方抛物线上的一点，求当△PAB面积最大时点P的坐标．
（3）M是直线AB上一动点，在平面直角坐标系内是否存在点N，使以O、B、M、N为顶点的四边形是菱形？若存在，请求出点N的坐标；若不存在，请说明理由．
【答案】（1）y=x+4．y=-
x2+4．（2）P（-2，3）．（3）N的坐标为（
，）或（-，-）或（-4，4）或（2，2）．
【解析】
试题分析：（1）设直线的解析式为y=kx+b，将A（-4，0），B（0，4）代入得到关于k、b的方程组，然后解得k、b的值即可；设抛物线的解析式为y=ax2+4，然后将点A的坐标代入求得a的值即可；
（2）过点P作PQ⊥x轴，交AB于点Q．设点P（a， -
+4），Q（a，a+4）．则PQ=--a，然后依据三角形的面积公式列出△ABP的面积与a的函数关系式，然后依据二次函数的性质求解即可；
（3）先根据题意画出图形，需要注意本题共有4种情况，然后依据菱形的性质、等腰直角三角形的性质以及特殊锐角三角函数值求解即可．
试题解析：（1）设直线的解析式为y=kx+b．
∵将A（-4，0），B（0，4）代入得：
，解得k=1，b=4，
∴直线AB的解析式为y=x+4．
设抛物线的解析式为y=ax2+4．
∵将A（-4，0）代入得：16a+4=0，解得a=-，
∴抛物线的解析式为y=-x2+4．
（2）如图1所示，过点P作PQ⊥x轴，交AB于点Q．
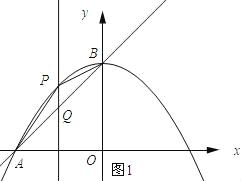
设点P的坐标为（a，- +4），则点Q的坐标为（a，a+4）．则PQ=-+4-（a+4）=--a．
∵S△ABP的面积=
PQ（xB-xA）=×4×（--a）=-a2-2a=-（a+2）2+2，
∴当a=-2时△ABP的面积最大，此时P（-2，3）．
（3）如图2所示：延长MN交x轴与点C．
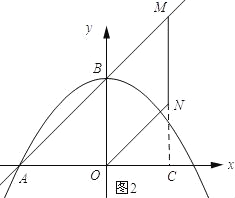
∵MN∥OB，OB⊥OC，
∴MN⊥OC．
∵OA=OB，∠AOB=90°，
∴∠BA0=45°．
∵ON∥AB，
∴∠NOC=45°．
∴OC=ON×
=4×=2
，NC=ON×=4×=2
．
∴点N的坐标为（2，2）．
如图3所示：过点N作NC⊥y轴，垂足为C．
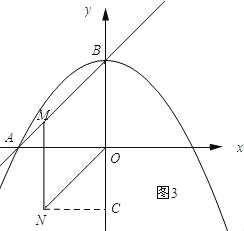
∵OA=OB，∠AOB=90°，
∴∠OBA=45°．
∵ON∥AB，
∴∠NOC=45°．
∴OC=ON×=4×=2，NC=ON×=4×=2．
∴点N的坐标为（-2，-2）．
如图4所示：连接MN交y轴与点C．
∵四边形BNOM为菱形，OB=4，
∴BC=OC=2，MC=CN，MN⊥OB．
∴点的纵坐标为2．
∵将y=2代入y=x+4得：x+4=2，解得：x=-2，
∴点M的坐标为（-2，2）．
∴点N的坐标为（2，2）．
如图5所示：
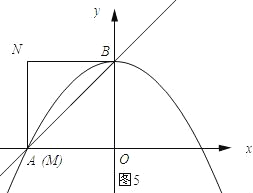
∵四边形OBNM为菱形，
∴∠NBM=∠ABO=45°．
∴四边形OBNM为正方形．
∴点N的坐标为（-4，4）．
综上所述点N的坐标为（，）或（-，-）或（-4，4）或（2，2）．
