题目内容
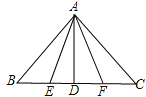
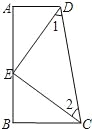
【题目】如图,AD∥BC,∠A=90°,E是AB上的一点,且AD=BE,∠1=∠2.
(1)Rt△ADE与Rt△BEC全等吗?请写出必要的推理过程;
(2)△CED是不是直角三角形?请说明理由;
(3)若已知AD=6,AB=14,请求出请求出△CED的面积.
【答案】(1)全等,见解析;(2)是,理由见解析;(3)50
【解析】
(1)由∠1=∠2,可得DE=CD,根据证明直角三角形全等的“HL”定理,证明即可;
(2)根据题意,∠AED+∠ADE=90°,∠BEC+∠BCE=90°,又∠AED=∠BCE,∠ADE=∠BEC,所以,∠AED+∠BEC=90°,即可证得∠DEC=90°,即可得出;
(3)由(1)可得BE=AD,所以可求出AE,根据勾股定理可求出DE,再由已知∠1=∠2和(2)可知)△CED是等腰直角三角形,从而求出△CED的面积
(1)Rt△ADE≌Rt△BEC;
理由如下:
∵∠1=∠2,
∴DE=CE,又∠A=∠B=90°,AE=BC
∴在Rt△ADE和Rt△BEC中,
DE=CE、AE=BC,
∴Rt△ADE≌Rt△BEC;
(2))△CDE是直角三角形;
理由如下:
∵Rt△ADE≌Rt△BEC,
∴∠AED=∠BCE,∠ADE=∠BEC,
又∵∠AED+∠ADE=90°,∠BEC+∠BCE=90°,
∴2(∠AED+∠BEC)=180°,
∴∠AED+∠BEC=90°,
∴∠DEC=90°,
∴△CDE是直角三角形;
(3)已知AD=BE=6,
∴AE=AB﹣BE=AB﹣AD=14﹣6=8,
在Rt△ADE中,
DE=![]()
![]() =10,
=10,
又∠1=∠2,
∴DE=CE=10,
再由(2)得:
△CED的面积为:![]() DECE=
DECE=![]() ×10×10=50.
×10×10=50.
所以△CED的面积为:50.
.

 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案【题目】近年来,我国很多地区持续出现雾霾天气.某社区为了调查本社区居民对雾霾天气主要成因的认识情况,随机对该社区部分居民进行了问卷调查,要求居民从五个主要成因中只选择其中的一项,被调查居民都按要求填写了问卷.社区对调查结果进行了整理,绘制了如下不完整的统计图表.被调查居民选择各选项人数统计表
雾霾天气的主要成因 | 频数(人数) |
A大气气压低,空气不流动 | m |
B地面灰尘大,空气湿度低 | 40 |
C汽车尾气排放 | n |
D工厂造成的污染 | 120 |
E其他 | 60 |
请根据图表中提供的信息解答下列问题:
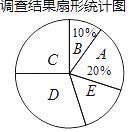
(1)填空:m=________,n=________,扇形统计图中C选项所占的百分比为________.
(2)若该社区居民约有6 000人,请估计其中会选择D选项的居民人数.
(3)对于“雾霾”这个环境问题,请你用简短的语言发出倡议.