题目内容
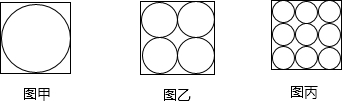
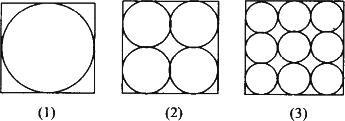
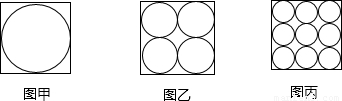
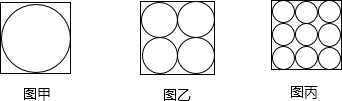
如图,在三个同样大小的正方形中,分别画一个内切圆.面积为S1(图甲所示);画四个半径相等、相邻两圆相互外切、与正方形各边都相切的圆,这四个圆的面积和为S4,(图乙所示);画九个半径相等、相邻两圆相互外切、边缘圆与正方形各边都相切的圆,这九个圆的面积之和为S9,(图丙所示);则S1,S4和S9的大小关系是
- A.S1最大
- B.S4最大
- C.S9最大
- D.一样大
D
分析:设正方形的边长是a,得出图甲中圆的半径是 a,图乙中圆的半径是
a,图乙中圆的半径是 a,图丙中圆的半径是
a,图丙中圆的半径是 a,根据圆的面积公式求出S1、S4、S9,再进行比较即可.
a,根据圆的面积公式求出S1、S4、S9,再进行比较即可.
解答:∵设正方形的边长是a,
则根据相切两圆的性质得出图甲中圆的半径是 a,图乙中圆的半径是
a,图乙中圆的半径是 ×
× a=
a= a,图丙中圆的半径是
a,图丙中圆的半径是 ×
× a=
a= a,
a,
∴S1=π× =
= πa2,
πa2,
S4=4×π×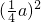 =
= πa2,
πa2,
S9=9×π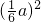 =
= πa2,
πa2,
∴S1=S4=S9.
故选D.
点评:本题考查了相切两圆的性质和圆的性质,主要考查学生能否根据相切两圆的性质得出图甲、图乙、图丙中各个圆的半径,题目具有一定的代表性,是一道比较好的题目.
分析:设正方形的边长是a,得出图甲中圆的半径是
 a,图乙中圆的半径是
a,图乙中圆的半径是 a,图丙中圆的半径是
a,图丙中圆的半径是 a,根据圆的面积公式求出S1、S4、S9,再进行比较即可.
a,根据圆的面积公式求出S1、S4、S9,再进行比较即可.解答:∵设正方形的边长是a,
则根据相切两圆的性质得出图甲中圆的半径是
 a,图乙中圆的半径是
a,图乙中圆的半径是 ×
× a=
a= a,图丙中圆的半径是
a,图丙中圆的半径是 ×
× a=
a= a,
a,∴S1=π×
 =
= πa2,
πa2,S4=4×π×
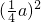 =
= πa2,
πa2,S9=9×π
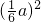 =
= πa2,
πa2,∴S1=S4=S9.
故选D.
点评:本题考查了相切两圆的性质和圆的性质,主要考查学生能否根据相切两圆的性质得出图甲、图乙、图丙中各个圆的半径,题目具有一定的代表性,是一道比较好的题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目