题目内容
枇杷是莆田名果之一,某果园有100棵枇杷树.每棵平均产量为40千克,现准备多种一些枇杷树以提高产量,但是如果多种树,那么树与树之间的距离和每一棵数接受的阳光就会减少,根据实践经验,每多种一棵树,投产后果园中所有的枇杷树平均每棵就会减少产量0.25千克,问:增种多少棵枇杷树,投产后可以使果园枇杷的总产量最多?最多总产量是多少千克?
【答案】分析:设增种x棵树,果园的总产量为y千克,列出二次函数等式可得.注意公式ymax=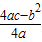 的运用.
的运用.
解答:解:设增种x棵树,果园的总产量为y千克
依题意得:
y=(100+x)(40-0.25x)
=4000-25x+40x-0.25x2
=-0.25x2+15x+4000
因为a=-0.25<0,
所以当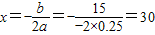 ,
,
y最大值=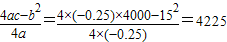
答;投产后可以使果园枇杷的总产量最多最多总产量是4225千克.
点评:先建立函数关系式,把它转化为二次函数的一般形式,然后根据二次函数的顶点坐标公式进行求极值.
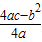 的运用.
的运用.解答:解:设增种x棵树,果园的总产量为y千克
依题意得:
y=(100+x)(40-0.25x)
=4000-25x+40x-0.25x2
=-0.25x2+15x+4000
因为a=-0.25<0,
所以当
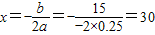 ,
,y最大值=
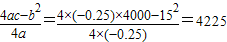
答;投产后可以使果园枇杷的总产量最多最多总产量是4225千克.
点评:先建立函数关系式,把它转化为二次函数的一般形式,然后根据二次函数的顶点坐标公式进行求极值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的顶点坐标是
的顶点坐标是