题目内容
将抛物线y=ax2+bx+c向左平移2个单位，再向下平移3个单位后得到抛物线y=2x2，则原抛物线是
- A.y=2x2-8x+11
- B.y=2x2-4x+7
- C.y=2x2+8x+3
- D.y=2x2-8x-5
A
分析：抛物线平移．不改变二次项系数，平移后抛物线的顶点坐标为（0，0），根据平移规律可推出原抛物线顶点坐标为（2，3），根据顶点式可求抛物线解析式．
解答：平移后抛物线y=2x2的顶点坐标为（0，0），
根据平移规律，得原抛物线顶点坐标为（2，3），
又平移不改变二次项系数，
∴原抛物线解析式为y=2（x-2）2+3，
即y=2x2-8x+11．
故选A．
点评：本题主要考查了函数图象的平移，抛物线与坐标轴的交点坐标的求法，要求熟练掌握平移的规律：左加右减，上加下减．并用规律求函数解析式．
分析：抛物线平移．不改变二次项系数，平移后抛物线的顶点坐标为（0，0），根据平移规律可推出原抛物线顶点坐标为（2，3），根据顶点式可求抛物线解析式．
解答：平移后抛物线y=2x2的顶点坐标为（0，0），
根据平移规律，得原抛物线顶点坐标为（2，3），
又平移不改变二次项系数，
∴原抛物线解析式为y=2（x-2）2+3，
即y=2x2-8x+11．
故选A．
点评：本题主要考查了函数图象的平移，抛物线与坐标轴的交点坐标的求法，要求熟练掌握平移的规律：左加右减，上加下减．并用规律求函数解析式．
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
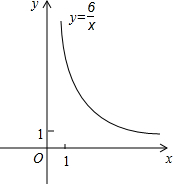（2011•西城区模拟）如图，平面直角坐标系xOy中，点pn（xn，yn）在双曲线
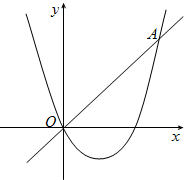已知抛物线y=ax2-2ax与直线l：y=ax（a＞0）的交点除了原点O外，还相交于另一点A．