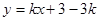题目内容
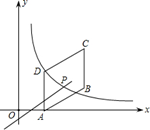
如图,直线y=x+b(b≠0)交坐标轴于A、B两点,点D在直线上,D的横纵坐标之积为2,过D作两坐标轴的垂线DC、DE,连接OD.
(1)求证:AD平分∠CDE;
(2)对任意的实数b(b≠0),求证:AD•BD为定值;
(3)是否存在直线AB,使得四边形OBCD为平行四边形?若存在,求出直线的解析式;若不存在,请说明理由.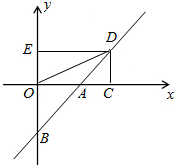
(1)证明见解析;(2)证明见解析;(3)存在,y=x-1.
解析试题分析:(1)由于DE⊥y轴,DC⊥x轴,不难得出∠EDC=90°,因此要证AD平分∠CDE,需证得∠ADC或∠ADE为45°,根据直线AB的解析式可得出A(-b,0),B(0,b),因此OA=OB,即三角形OAB是等腰直角三角形,即可证得∠ADC=∠ABO=45°,由此可得证;
(2)在(1)中已经证得三角形ADC是等腰三角形,同理可得出三角形BDE也是等腰三角形,因此AD= CD,BD=
CD,BD= DE,那么AD•BD=2CD•DE,而CD和DE的长,正好是反比例函数图象上D点的横坐标与纵坐标,由此可得出AD•BD是个定值;
DE,那么AD•BD=2CD•DE,而CD和DE的长,正好是反比例函数图象上D点的横坐标与纵坐标,由此可得出AD•BD是个定值;
(3)如果四边形OBCD是平行四边形,需要满足的条件是OB=CD,OA=AC,可根据这个条件设B、D的坐标,然后将D点坐标代入反比例函数的解析式中,即可求出D点坐标,也就得出了B点的坐标,然后用待定系数法即可求得直线的解析式.
试题解析:(1)证明:由y=x+b得A(-b,0),B(0,b).
∴∠DAC=∠OAB=45°
又∵DC⊥x轴,DE⊥y轴
∴∠ACD=∠CDE=90°
∴∠ADC=45°
即AD平分∠CDE.
(2)证明:∵∠ACD=90°,∠ADC=45°,
∴△ACD是等腰直角三角形,
同理可得,△BDE是等腰直角三角形,
∴AD= CD,BD=
CD,BD= DE.
DE.
∴AD•BD=2CD•DE=2×2=4为定值.
(3)解:存在直线AB,使得OBCD为平行四边形.
若OBCD为平行四边形,则AO=AC,OB=CD.
由(1)知AO=BO,AC=CD,
设OB=a(a>0),
∴B(0,-a),D(2a,a),
∵D的横纵坐标之积为2,
∴点D在双曲线y=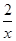 上,
上,
∴2a•a=2,
∴a1=-1(舍去),a2=1,
∴B(0,-1).
又∵B在y=x+b上,
∴b=-1.
即存在直线:y=x-1,使得四边形OBCD为平行四边形.
考点:1.一次函数综合题;2.等腰直角三角形;3.平行四边形的判定与性质.

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案为了节约资源,科学指导居民改善居住条件,小王向房管部门提出了一个购买商品房的政策性方案.
| 人均住房面积(平方米) | 单价(万元/平方米) |
| 不超过30(平方米) | 0.3 |
| 超过30平方米不超过m(平方米)部分(45≤m≤60) | 0.5 |
| 超过m平方米部分 | 0.7 |
根据这个购房方案:
(1)若某三口之家欲购买120平方米的商品房,求其应缴纳的房款;
(2)设该家庭购买商品房的人均面积为x平方米,缴纳房款y万元,请求出y关于x的函数关系式;
(3)若该家庭购买商品房的人均面积为50平方米,缴纳房款为y万元,且57<y≤60 时,求m的取值范围.
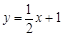 的图象与
的图象与 轴交于点
轴交于点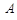 ,与
,与 轴交于点
轴交于点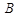 .
.  ,
, 两点的坐标;
两点的坐标;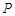 ,且使△A
,且使△A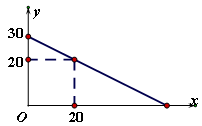
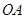 和
和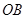 分别表示某日从上午8点到上午11点,每个普通售票窗口售出的车票数
分别表示某日从上午8点到上午11点,每个普通售票窗口售出的车票数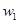 (张)和每个无人售票窗口售出的车票数
(张)和每个无人售票窗口售出的车票数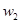 (张)关于售票时间
(张)关于售票时间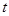 (小时)的函数图象.
(小时)的函数图象.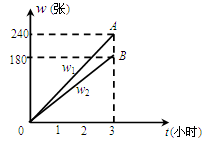
 的图象与x轴、y轴分别交于点A,B,与函数y=x的图象交于点M,点M的横坐标为2.在x轴上有一点P (a,0)(其中a>2),过点P作x轴的垂线,分别交函数
的图象与x轴、y轴分别交于点A,B,与函数y=x的图象交于点M,点M的横坐标为2.在x轴上有一点P (a,0)(其中a>2),过点P作x轴的垂线,分别交函数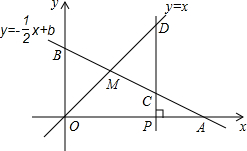
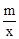 (x>0)的函数图象经过点D,点P是一次函数
(x>0)的函数图象经过点D,点P是一次函数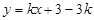
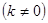 的图象与该反比例函数图象的一个公共点.
的图象与该反比例函数图象的一个公共点.