题目内容
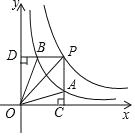
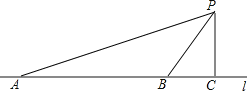
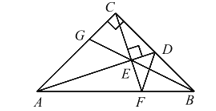
【题目】如图:Rt△ABC 中,AC=BC,∠ACB=90°,D 为 BC 边中点,CF⊥AD 交 AD 于 E,交 AB 于 F,BE交 AC 于 G,连 DF,下列结论:①AC=AF,②CD+DF=AD,③∠ADC=∠BDF,④CE=BE,⑤∠ BED=45°,其中正确的有( )
A. 5 个B. 4 个C. 3 个D. 2 个
【答案】D
【解析】
如图,作BH⊥BC交CF的延长线于H,作BN⊥AD交AD的延长线于N,BM⊥CH于M.想办法证明△ACD≌△CBH(ASA),△BFD≌△BFH(SAS),△ACE≌△CBE(AAS),△CDE≌△BDN(AAS),利用全等三角形的性质一一判断即可.
如图,作BH⊥BC交CF的延长线于H,作BN⊥AD交AD的延长线于N,BM⊥CH于M.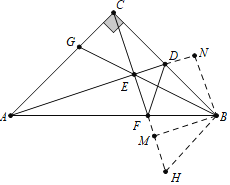
∵AD⊥CF,BH⊥BC,
∴∠ACD=∠CBH=∠AEC=90°,
∵∠CAD+∠ACE=90°,∠ACE+∠BCH=90°,
∴∠CAD=∠BCH,
∵CA=CB,
∴△ACD≌△CBH(ASA),
∴∠ADC=∠H,CD=BH,AD=CH,
∵CD=BD,
∴∠BD=BH,
∵∠FBD=∠FBH=45°,BF=BF,
∴△BFD≌△BFH(SAS),
∴∠H=∠BDF,DF=FH,
∴∠ADC=∠BDF,故③正确,
∵AD=CH,CH=FH+CF=DF+CF,
∵CF>CD,
∴AD≠DF+CD,故②错误,
假设①成立,则∵AE⊥CF,
∴CE=EF,∵CD=DB,
∴DE∥BF,显然与已知矛盾,故①错误,
∵∠CAE=∠BCM,∠AEC=∠CMB,AC=BC,
∴△ACE≌△CBE(AAS),
∴CE=BM,
∵BE>BM,
∴CE≠BE,故④错误,
∵∠CED=∠N=90°,∠CDE=∠BDN,CD=BD,
∴△CDE≌△BDN(AAS),
∴CE=BN,
∵EC=BM,
∴BM=BN,∵BM⊥EH,BN⊥EN,
∴BE平分∠NEH,
∵∠NEH=90°
∴∠BEF=![]() ×90°=45°.故⑤正确.
×90°=45°.故⑤正确.
故选:D.

 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案【题目】解决问题:
小川同学乘坐新开通的C2701次城际列车,它从“北京西”站始发直达终点“大兴机场”站,但因列车行驶的全程分别属于两段不同的路网A段和新开通运营的B段,在两段运行的平均速度有所不同,小川搜集了相关信息填入下表.
线路划分 | A段 | B段(新开通) |
所属全国铁路网 | 京九段 | 京雄城际铁路北京段 |
站间 | 北京西—李营 | 李营—大兴机场 |
里程近似值(单位:km) | 15 | 33 |
运行的平均速度(单位:km/h) | ||
所用时间(单位:h) |
已知C2701次列车在B段运行的平均速度比在A段运行的平均速度快35km/h,在B段运行所用时间是在A段运行所用时间的1.5倍,C2701次列车从“北京西”站到“大兴机场”站全程需要多少小时?(提示:可借助表格解决问题)