Question

【题目】如果关于 x 的一元二次方程 a+bx+c＝0（a≠0）有两个实数根，且其中一个根比另一个根大 1，那么称这样的方程为“邻根方程”．例如，一元二次方程+x＝0 的两个根是 ＝0，＝﹣1，则方程 +x＝0 是“邻根方程”．

（1）通过计算，判断下列方程是否是“邻根方程”：

①﹣x﹣6＝0；

②2﹣2x+1＝0．

（2）已知关于 x 的方程﹣（m﹣1）x﹣m＝0（m 是常数）是“邻根方程”，求 m 的值；

（3）若关于 x 的方程 a+bx+1＝0（a、b 是常数，a＞0）是“邻根方程”，令 t＝8a-，试求 t 的最大值．

Answer 1

【答案】（1）不是邻根方程；是邻根方程（2）或（3）

【解析】

（1）分别解出方程的根，令两根相减，根据邻根方程的定义进行判断即可得解；

（2）解出方程的根，令两根差的绝对值等于，从而得到关于的方程，解方程即可；

（3）利用根与系数的关系表示出，进一步化简可得，整体代入再配方可得，即可确定的最大值．

解：（1）①

，

∴，

∵

∴不符合邻根方程的定义

∴不是邻根方程．

②

∵，，

∴

∴

∴，

∴

∴符合邻根方程的定义

∴是邻根方程．

（2）∵关于的方程（ 是常数）是邻根方程

∴解方程可得：，

∴

∴，

∴或．

（3）∵关于的方程（、 是常数，）是邻根方程，设两个根为、

∴

∵，

∴

∴

∴

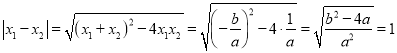
∴当时，．

故答案是：（1）不是邻根方程；是邻根方程（2）或（3）