题目内容
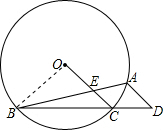
已知:如图,⊙O的内接△ABC中,∠BAC=45°,∠ABC=15°,AD∥OC并交BC的延长线于D,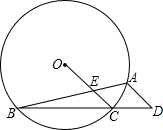 OC交AB于E.
OC交AB于E.
(1)求∠D的度数;
(2)求证:AC2=AD•CE;
(3)求
的值.
 OC交AB于E.
OC交AB于E.(1)求∠D的度数;
(2)求证:AC2=AD•CE;
(3)求
| BC |
| CD |
(1)如图,连接OB(1分)
∵⊙O的内接△ABC中,∠BAC=45°,
∴∠BOC=2∠BAC=90°
∵OB=OC,
∴∠OBC=∠OCB=45°
∵AD∥OC,
∴∠D=∠OCB=45°(2分)
(2)证明:∵∠BAC=45°,∠D=45°,
∴∠BAC=∠D(3分)
∵AD∥OC,
∴∠ACE=∠DAC(4分)
∴△ACE∽△DAC
∴
=
∴AC2=AD•CE(5分)
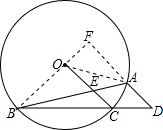
(3)方法一:如图,延长BO交DA的延长线于F,连接OA
∵AD∥OC,
∴∠F=∠BOC=90°
∵∠ABC=15°,
∴∠OBA=∠OBC-∠ABC=30°
∵OA=OB,
∴∠FOA=∠OBA+∠OAB=60°,∠OAF=30°、
∴OF=
OA
∵AD∥OC,
∴△BOC∽△BFD
∴
=
∴
=
=
=2,即
的值为2(7分)
方法二:作OM⊥BA于M,设⊙O的半径为r,可得BM=
r,OM=
,∠MOE=30°,
ME=OM•tan30°=
r,BE=
r,AE=
r,所以
=
=2
∵⊙O的内接△ABC中,∠BAC=45°,
∴∠BOC=2∠BAC=90°
∵OB=OC,
∴∠OBC=∠OCB=45°
∵AD∥OC,
∴∠D=∠OCB=45°(2分)
(2)证明:∵∠BAC=45°,∠D=45°,
∴∠BAC=∠D(3分)
∵AD∥OC,
∴∠ACE=∠DAC(4分)
∴△ACE∽△DAC
∴
| AC |
| DA |
| CE |
| AC |
∴AC2=AD•CE(5分)

(3)方法一:如图,延长BO交DA的延长线于F,连接OA
∵AD∥OC,
∴∠F=∠BOC=90°
∵∠ABC=15°,
∴∠OBA=∠OBC-∠ABC=30°
∵OA=OB,
∴∠FOA=∠OBA+∠OAB=60°,∠OAF=30°、
∴OF=
| 1 |
| 2 |
∵AD∥OC,
∴△BOC∽△BFD
∴
| BC |
| BD |
| BO |
| BF |
∴
| BC |
| CD |
| BO |
| OF |
| OA |
| OF |
| BC |
| CD |
方法二:作OM⊥BA于M,设⊙O的半径为r,可得BM=
| ||
| 2 |
| r |
| 2 |
ME=OM•tan30°=
| ||
| 6 |
2
| ||
| 3 |
| ||
| 3 |
| BC |
| CD |
| BE |
| EA |


练习册系列答案
相关题目
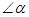 等于 ▲ °.
等于 ▲ °.