题目内容
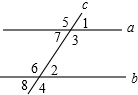
 12、如图,直线a,b都与c相交,给出条件,①∠1=∠2,②∠3=∠6,③∠4+∠7=180°④∠5+∠8=180°,其中能判断a∥b的条件是
12、如图,直线a,b都与c相交,给出条件,①∠1=∠2,②∠3=∠6,③∠4+∠7=180°④∠5+∠8=180°,其中能判断a∥b的条件是①②③④
(只填序号).分析:四个都可以判定a∥b:
(1)利用同位角相等判定两直线平行;
(2)利用内错角相等判定两直线平行;
(3)∠6与∠4是对顶角相等,再利用∠6+∠7=180°,同旁内角互补判定两直线平行;
(4)∠5与∠7互补,再利用∠7=∠8,同位角相等判定两直线平行.
(1)利用同位角相等判定两直线平行;
(2)利用内错角相等判定两直线平行;
(3)∠6与∠4是对顶角相等,再利用∠6+∠7=180°,同旁内角互补判定两直线平行;
(4)∠5与∠7互补,再利用∠7=∠8,同位角相等判定两直线平行.
解答:解:
①∵∠1=∠2,
∴a∥b(同位角相等,两直线平行);
②∵∠3=∠6,
∴a∥b(内错角相等,两直线平行);
③∵∠6=∠4(对顶角相等),
又∵∠4+∠7=180°,
∴∠6+∠7=180°,
∴a∥b(同旁内角互补,两直线平行);
④∵∠5+∠7=180°(邻补角的定义),
又∵∠5+∠8=180°,
∴∠7=∠8,
∴a∥b(同位角相等,两直线平行).
①∵∠1=∠2,
∴a∥b(同位角相等,两直线平行);
②∵∠3=∠6,
∴a∥b(内错角相等,两直线平行);
③∵∠6=∠4(对顶角相等),
又∵∠4+∠7=180°,
∴∠6+∠7=180°,
∴a∥b(同旁内角互补,两直线平行);
④∵∠5+∠7=180°(邻补角的定义),
又∵∠5+∠8=180°,
∴∠7=∠8,
∴a∥b(同位角相等,两直线平行).
点评:正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
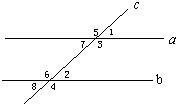
 13、如图,直线a、b都与直线c相交,给出下列条件:(1)∠l=∠2;(2)∠3=∠6;(3)∠4+∠7=180°;(4)∠5+∠8=180°,其中能判断a∥b的是( )
13、如图,直线a、b都与直线c相交,给出下列条件:(1)∠l=∠2;(2)∠3=∠6;(3)∠4+∠7=180°;(4)∠5+∠8=180°,其中能判断a∥b的是( ) 8、如图,直线a、b都与c相交,由下列条件能推出a∥b的是( )
8、如图,直线a、b都与c相交,由下列条件能推出a∥b的是( ) 如图,直线a、b都与直线c相交,给出下列条件:
如图,直线a、b都与直线c相交,给出下列条件: