��Ŀ����
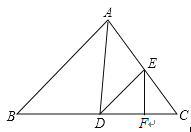
����Ŀ��ij��˾������һ���µĽ��ܲ�Ʒ���ò�Ʒ�ijɱ���Ϊ6Ԫ/�����ò�Ʒ����ʽͶ���г�ǰͨ�������������Ϊ��һ���£�30�죩����Ӫ�����ۼ�Ϊ8Ԫ/����������Ա��������������˸��ټ�¼��������¼������ͼ��ͼ�е�����ODE��ʾ��������y������������ʱ��x���죩֮��ĺ�����ϵ����֪�߶�DE��ʾ�ĺ�����ϵ�У�ʱ��ÿ����1�죬������������5���� 
��1����24�����������������������������Ԫ��
��2����y��x֮��ĺ�����ϵʽ����д��x��ȡֵ��Χ��
��3��������������640Ԫ���������ж����죿�������ڼ䣬��������������Ƕ���Ԫ��
���𰸡�
��1��330��660
��2���⣺���߶�OD����ʾ��y��x֮��ĺ�����ϵʽΪy=kx��
����17��340������y=kx��
340=17k����ã�k=20��
���߶�OD����ʾ��y��x֮��ĺ�����ϵʽΪy=20x��
��������ã��߶�DE����ʾ��y��x֮��ĺ�����ϵʽΪy=340��5��x��22��=��5x+450��
�������߶�����ʾ�ĺ�����ϵʽ�ɷ����飬
�� ![]() ����ã�
����ã� ![]() ��
��
�ཻ��D������Ϊ��18��360����
��y��x֮��ĺ�����ϵʽΪy= ![]() ��
��
��3���⣺��0��x��18ʱ����������ã���8��6����20x��640��
��ã�x��16��
��18��x��30ʱ����������ã���8��6��������5x+450����640��
��ã�x��26��
��16��x��26��
26��16+1=11���죩��
��������������640Ԫ����������11�죮
�ߵ�D������Ϊ��18��360����
�������������Ϊ360����
360��2=720��Ԫ����
���������ڼ䣬���������������720Ԫ��
���������⣺��1��340����24��22����5=330�������� 330����8��6��=660��Ԫ����
���Դ��ǣ�330��660��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�