ћвƒњƒЏ»Ё
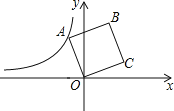
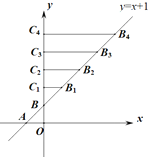
°Њћвƒњ°њ»зЌЉ£ђ‘Џ∆љ√ж÷±љ«„ш±кѕµxOy÷–£ђ“їіќЇѓ эy=x+1”лx°Ґy ÷бЈ÷±рљї”ЏµгA°ҐB£ђ‘Џ÷±ѕя AB…ѕљЎ»°BB1=AB£ђєэµгB1Ј÷±р„чy ÷бµƒієѕя£ђіє„гќ™µгC1£ђµ√µљ®SBB1C1£ї‘Џ÷±ѕя AB…ѕљЎ»°B1B2= BB1£ђєэµгB2Ј÷±р„чy ÷бµƒієѕя£ђіє„гќ™µгC2£ђµ√µљ®SBB2C2£ї‘Џ÷±ѕяAB…ѕљЎ»°B2B3= B1B2£ђєэµгB3„чy ÷бµƒієѕя£ђіє„гќ™µгC3£ђµ√µљ®SBB3C3£ї°≠°≠£їµЏ3Єц®SBB3C3µƒ√жїэ «___________£їµЏnЄц®SBBnCnµƒ√жїэ «______________£®”√Їђnµƒ љ„”±н Њ£ђn «’э’ы э£©£Ѓ
°Њір∞Є°њ![]() £ђ
£ђ ![]()
°Њљвќц°њ
ѕ»«у≥цA°ҐBЅљµгµƒ„ш±к£ђ‘ў…иB1(a,a+1)£ђB2(b,b+1)£ђB3(c,c+1)£ђ«у≥цa°Ґb°Ґcµƒ÷µ£ђјы”√»эљ«–ќµƒ√жїэєЂ љµ√≥ц∆д√жїэ£ђ’“≥цєж¬…Љіњ…£Ѓ
љв£Ї°я“їіќЇѓ эy=x+1”лx°Ґy ÷бЈ÷±рљї”ЏµгA°ҐB£ђ
°аA(-1,0)£ђB(0,1)£ђ
°а![]() £ђ
£ђ
…иB1(a,a+1)£ђB2(b,b+1)£ђB3(c,c+1)£ђ
°яBB1=AB
°аa 2+ (a+1-1)2=2
°аB1(1,2)£ђ
Ќђјнњ…µ√£ђB2(2,3)£ђB3(3,4)£ђ
°а![]()
![]()
![]()
°≠°≠
![]()
є ір∞Єќ™£Ї![]() £ђ
£ђ![]()

ЅЈѕ∞≤бѕµЅ–ір∞Є
ѕаєЎћвƒњ