题目内容
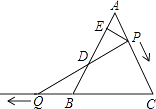
【题目】如图,∠ABC=90°,∠EBE′=90°,AB=BC,BE=BE′,若AE=1,BE=2,∠BE′C=135°,求EC的长.
【答案】解:∵∠ABE+∠EBC=∠ABC=90°,
∠E'BC+∠EBC=∠E'BE=90°,
∴∠ABE=∠E'BC,
在△ABE与△CBE'中, ,
,
∴△ABE≌△CBE'(SAS),
∴CE'=AE=1,
∵∠EBE'=90°,BE=BE'=2,
∴EE'2=22+22=8,
∵∠EBE'=90°,BE=BE',
∴∠BE'E=45°,
∵∠BE'C=135°,
∴∠EE'C=135°﹣45°=90°,
∴ ![]()
【解析】(1)根据∠ABC=90°,∠EBE′=90°,先证明∠ABE=∠E'BC,再利用全等三角形的判定证明△ABE≌△CBE',得出CE'=AE,然后证明∠EE'C=90°,利用勾股定理求出EE',在Rt△EE'C中,根据勾股定理求出EC的长即可。

练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目