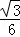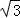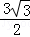题目内容
小华同学学习了第二十五章《锐角三角比》后,对求三角形的面积方法进行了研究,得到了新的结论:
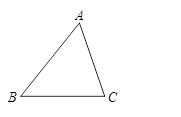
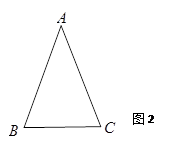
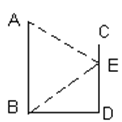
(1)如图1,已知锐角△ABC.求证: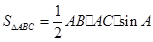 ;(2)根据题(1)得到的信息,请完成下题:如图2,在等腰△ABC中,AB=AC=12厘米,点P从A点出发,沿着边AB移动,点Q从C点出发沿着边CA移动,点Q的速度是1厘米/秒,点P的速度是点Q速度的2倍,若它们同时出发,设移动时间为t秒,问:当t为何值时,
;(2)根据题(1)得到的信息,请完成下题:如图2,在等腰△ABC中,AB=AC=12厘米,点P从A点出发,沿着边AB移动,点Q从C点出发沿着边CA移动,点Q的速度是1厘米/秒,点P的速度是点Q速度的2倍,若它们同时出发,设移动时间为t秒,问:当t为何值时, ?
?

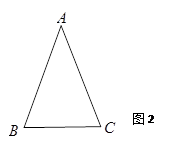
(1)如图1,已知锐角△ABC.求证:
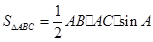 ;(2)根据题(1)得到的信息,请完成下题:如图2,在等腰△ABC中,AB=AC=12厘米,点P从A点出发,沿着边AB移动,点Q从C点出发沿着边CA移动,点Q的速度是1厘米/秒,点P的速度是点Q速度的2倍,若它们同时出发,设移动时间为t秒,问:当t为何值时,
;(2)根据题(1)得到的信息,请完成下题:如图2,在等腰△ABC中,AB=AC=12厘米,点P从A点出发,沿着边AB移动,点Q从C点出发沿着边CA移动,点Q的速度是1厘米/秒,点P的速度是点Q速度的2倍,若它们同时出发,设移动时间为t秒,问:当t为何值时, ?
?(1)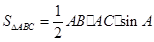 ; (2)当t=3秒时,
; (2)当t=3秒时, .
.
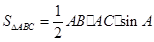 ; (2)当t=3秒时,
; (2)当t=3秒时, .
.试题分析:(1)首先过点C作CE⊥AB于点E,则sinA=
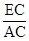 ,进而得出EC的长,即可得出答案;
,进而得出EC的长,即可得出答案;(2)首先表示出△APQ的面积,进而得出△ABC的面积,进而利用
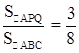 ,求出t的值即可.
,求出t的值即可.试题解析:
(1)如图1,过点C作CD⊥AB于点D
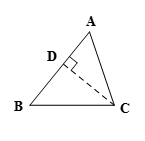
在Rt△ADC中,sinA=
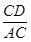
∴CD=AC.sinA
∵
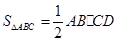
∴
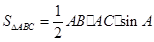 .
.(2)根据题意:AP=2t厘米 ,CQ=t厘米
∴AQ=(12—t)厘米
由(1)得:
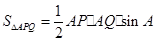
∴
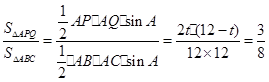
化简得:
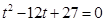
解得
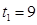 (舍),
(舍),
即当t=3秒时,
 .
.

练习册系列答案
相关题目

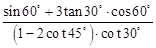 .
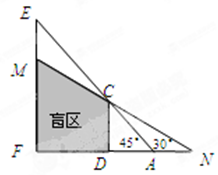
. ,则AB长为____米.
,则AB长为____米.
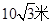 ; (B)
; (B)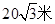 ; (C)
; (C)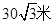 ; (D)60米。
; (D)60米。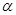 、
、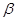 都是锐角,如果
都是锐角,如果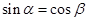 ,那么
,那么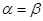 ;
;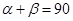 °;
°;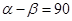 °;
°;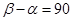 °.
°.