题目内容
在半径为2的圆中，长为2
的弦所对的圆心角的度数是（ ）
| 3 |
| A、60° | B、90° |
| C、120° | D、135° |
分析：如图，先利用垂径定理得出AD=
，再解直角三角形可得∠AOD=60°，再得∠AOB=120°．
| 3 |
解答：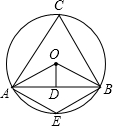
解：如图，AB=2
，连接OA，OB，作OD⊥AB，垂足为D．
则由垂径定理知，点D是AB的中点，AD=
，
∴sin∠AOD=
=
，
∴∠AOD=60°，∠AOB=120°．
故选C．
解：如图，AB=2| 3 |
则由垂径定理知，点D是AB的中点，AD=
| 3 |
∴sin∠AOD=
| AD |
| AO |
| ||
| 2 |
∴∠AOD=60°，∠AOB=120°．
故选C．
点评：本题利用了垂径定理、正弦的概念、圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．注意点C的位置有两种情况．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在半径为6cm的圆中，长为2πcm的弧所对的圆周角的度数是（ ）
| A、30° | B、45° | C、60° | D、90° |
在半径为1的圆中，长为
的弦所对的劣孤为（ ）
| 2 |
| A、π | ||
B、
| ||
C、
| ||
D、
|