题目内容
【题目】△ABC的两条中线AD、BE交于点F,连接CF,若△ABC的面积为24,则△ABF的面积为( ) 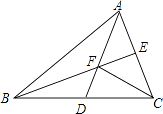
A.10
B.8
C.6
D.4
【答案】B
【解析】解∵AD是中线, ∴S△ABD=S△ADC= ![]() S△ABC ,
S△ABC ,
∵S△ABC=24,
∴S△ABD=S△ADC= ![]() ×24=12,
×24=12,
同理S△ABE=12,
∴S△ABD=S△ABE ,
∴S△ABD﹣S△ABF=S△ABE﹣S△ABF ,
即S△AEF=S△BDF ,
∵D是中点,
∴S△BDF=S△DFC ,
同理S△AEF=S△EFC ,
∴S△AEF=S△EFC=S△DFC= ![]() S△ADC=
S△ADC= ![]() ×12=4,
×12=4,
∴S△ABF=S△ABD﹣S△BDF=12﹣4=8,
故选B.
【考点精析】关于本题考查的三角形的面积,需要了解三角形的面积=1/2×底×高才能得出正确答案.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目