题目内容
【题目】如图,直线AB、CD相交于点O,OF平分∠AOE,OF⊥CD,垂足为O.
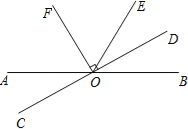
(1)若∠AOE=120°,求∠BOD的度数;
(2)写出图中所有与∠AOD互补的角: .
【答案】(1)30°;(2)∠AOC、∠BOD、∠DOE.
【解析】试题分析:(1)根据角平分线的性质可得∠AOF=![]() ∠AOE=60°,再由OF⊥CD,可得∠COF=90°,再根据角的和差关系可得∠AOC的度数,根据对顶角相等可得答案;
∠AOE=60°,再由OF⊥CD,可得∠COF=90°,再根据角的和差关系可得∠AOC的度数,根据对顶角相等可得答案;
(2)根据两个角的和为180°即为互补可得答案.
解:(1)∵OF平分∠AOE,∠AOE=120°,
∴∠AOF=![]() ∠AOE=60°.
∠AOE=60°.
∵OF⊥CD,
∴∠COF=90°,
∴∠AOC=∠COF﹣∠AOF=30°,
∵∠AOC和∠BOD是对顶角,
∴∠BOD=∠AOC=30°;
(2)与∠AOD互补的角有∠AOC、∠BOD、∠DOE,
故答案为:∠AOC、∠BOD、∠DOE.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案
相关题目