题目内容
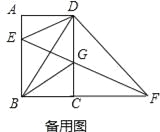
【题目】如图，在矩形ABCD中，BC=1，∠CBD=60°，点E是AB边上一动点（不与点A，B重合），连接DE，过点D作DF⊥DE交BC的延长线于点F，连接EF交CD于点G．
（1）求证：△ADE∽△CDF；
（2）求∠DEF的度数；
（3）设BE的长为x，△BEF的面积为y．
①求y关于x的函数关系式，并求出当x为何值时，y有最大值；
②当y为最大值时，连接BG，请判断此时四边形BGDE的形状，并说明理由．
【答案】（1）证明见解析；
（2）∠DEF=60°；
（3）①y=﹣（x﹣
）2+，
∴当x为时，y有最大值；
②四边形BGDE是平行四边形．
【解析】试题分析：（1）根据平行四边形的性质得到∠A=∠ADC=∠DCB=90°，根据余角的性质得到∠ADE=∠CDF，由相似三角形的判定定理即可得到结论；
（2）解直角三角形得到CD=
，根据矩形的性质得到AD=BC=1．AB=CD=，根据相似三角形的性质得到
=
，根据三角函数的定义即可得到结论；
（3）①根据相似三角形的性质得到CF=3﹣x，根据三角形的面积公式得到函数的解析式，根据二次函数的顶点坐标即可得到结论；②根据当x为时，y有最大值，得到BE=，CF=1，BF=2，根据相似三角形的想得到CG=，于是得到BE=DG，由于BE∥DG，即可得到结论．
试题解析：（1）在矩形ABCD中，
∵∠A=∠ADC=∠DCB=90°，
∴∠A=∠DCF=90°，
∵DF⊥DE，
∴∠A=∠EDF=90°，
∴∠ADE=∠CDF，
∴△ADE∽△CDF；
（2）∵BC=1，∠DBC=60°，
∴CD=，
在矩形ABCD中，
∵AD=BC=1．AB=CD=，
∵△ADE∽△CDF，
∴
，
∵tan∠DEF=
，
∴=，
∴∠DEF=60°；
（3）①∵BE=x，
∴AE=﹣x，
∵△ADE∽△CDF，
∴
，
∴CF=3﹣x，
∴BF=BC+CF=4﹣x，
∴y=
BEBF=x（4﹣x）=﹣
x2+2x，
∵y=﹣x2+2x=﹣（x﹣
）2+，
∴当x为时，y有最大值；
②y为最大值时，此时四边形BGDE是平行四边形，
∵当x为时，y有最大值，
∴BE=，CF=1，BF=2，
∵CG∥BE，
∴△CFG∽△BFE，
∴
，
∴CG=
，
∴DG=，
∴BE=DG，∵BE∥DG，
∴四边形BGDE是平行四边形．
