题目内容
如图,某商标 是由边长均为2的正三角形、正方形、正六边形的金属薄片镶嵌而成的镶嵌图案.
是由边长均为2的正三角形、正方形、正六边形的金属薄片镶嵌而成的镶嵌图案.
(1)求这个镶嵌图案中一个正三角形的面积;
(2)如果在这个镶嵌图案中随机确定一个点O,那么点O落在镶嵌图案中的正方形区域的概率为多少?(结果保留二位小数)
 是由边长均为2的正三角形、正方形、正六边形的金属薄片镶嵌而成的镶嵌图案.
是由边长均为2的正三角形、正方形、正六边形的金属薄片镶嵌而成的镶嵌图案.(1)求这个镶嵌图案中一个正三角形的面积;
(2)如果在这个镶嵌图案中随机确定一个点O,那么点O落在镶嵌图案中的正方形区域的概率为多少?(结果保留二位小数)

.解:(1)∵图案中正三角形的边长为2,∴高为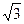 .(1分)
.(1分)
∴正三角形的面积为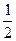 ×2×
×2×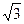 =
= 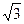 . (2分)
. (2分)
(2)∵图中共有11个正方形, ∴图中正方形的面积和为11×(2×2)=44. (3分)
∵图中共有2个正六边形,∴图中正六边形的面积和为2×(6×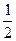 ×2×
×2× 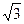
 )=12
)=12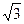 .(4分)∵图中共有10个正三角形,∴图中正三角形的
.(4分)∵图中共有10个正三角形,∴图中正三角形的 面积和为10
面积和为10 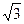 .
.
∵镶嵌图形的总面积为44+10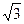 +12
+12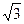 =44+22
=44+22 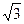 (5分)≈81.4,
(5分)≈81.4,
∴点O落在镶嵌图案中正方形区域的概率为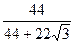 (7分)≈0.54.(8分)
(7分)≈0.54.(8分)
答:点O落在镶嵌图案中正方形区域的概率为0.54.(“≈”写为“=”不扣分)
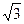 .(1分)
.(1分)∴正三角形的面积为
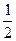 ×2×
×2×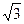 =
= 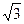 . (2分)
. (2分)(2)∵图中共有11个正方形, ∴图中正方形的面积和为11×(2×2)=44. (3分)
∵图中共有2个正六边形,∴图中正六边形的面积和为2×(6×
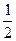 ×2×
×2× 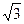
 )=12
)=12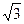 .(4分)∵图中共有10个正三角形,∴图中正三角形的
.(4分)∵图中共有10个正三角形,∴图中正三角形的 面积和为10
面积和为10 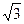 .
.∵镶嵌图形的总面积为44+10
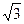 +12
+12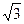 =44+22
=44+22 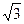 (5分)≈81.4,
(5分)≈81.4,∴点O落在镶嵌图案中正方形区域的概率为
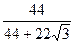 (7分)≈0.54.(8分)
(7分)≈0.54.(8分)答:点O落在镶嵌图案中正方形区域的概率为0.54.(“≈”写为“=”不扣分)
略

练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
 图,AB是⊙O的直径,点C,D都在⊙O上,连接CA,CB,DC,DB.已知∠D=30°,BC=3,则AB的长是 .
图,AB是⊙O的直径,点C,D都在⊙O上,连接CA,CB,DC,DB.已知∠D=30°,BC=3,则AB的长是 .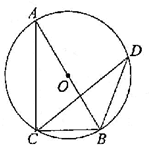
 B.
B. -4
-4
 中,以点(-3,4)为圆心,4为半径的圆
中,以点(-3,4)为圆心,4为半径的圆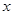 轴相交,与
轴相交,与 轴相切
轴相切
 的直径
的直径 过弦
过弦 的中点G,∠EOD=40°,则∠FCD的度数为 .
的中点G,∠EOD=40°,则∠FCD的度数为 .